机器学习笔记

        这里，我们只针对马尔可夫决策过程是有限状态、有限动作的情况，|S| < ∞， |A| < ∞。

        一、值迭代法：

1、 将每一个 s 的 V(s)初始化为 0
2、 循环直到收敛  {

对于每一个状态 s,对 V(s)做更新

}

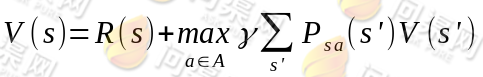
内循环的实现有两种策略:

1、 同步迭代法
        拿初始化后的第一次迭代来说，初始状态所有的 V(s)都为 0。然后对所有的 s 都计算新的 V(s)=R(s)+0=R(s)。在计算每一个状态时,得到新的 V(s)后，先存下来，不立即更新。待所有的 s 的新值(s)都计算完毕后，再统一更新。这样第一次迭代后V(s)=R(s)。
2、 异步迭代法
        与同步迭代对应的就是异步迭代了，对每一个状态 s，得到新的 V(s)后，不存储直接更新。第一次迭代后，大部分 V(s)>R(s)。

        不管使用这两种的哪一种，最终 V(s)会收敛到 V*(s)。知道了 V*后，我们再来求出相应的最优策略π* ，当然π*可以在求 V*的过程中求出。

        二、策略迭代法：

        值迭代法使V值收敛到V*，而策略迭代法关注π，使π收敛到π*。

1、 将随机指定一个 S 到 A 的映射π。
2、 循环直到收敛 {
                (a) 令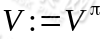
                (b) 对于每一个状态 s，对π(s)做更新
                        
        }

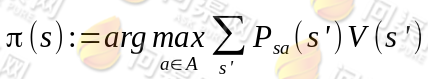
        (a)步中的 V 可以通过之前的 Bellman 等式求得

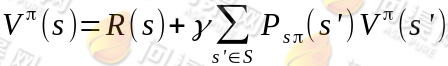
        这一步会求出所有状态 s 的。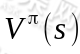
        (b)步实际上就是根据(a)步的结果挑选出当前状态 s 下，最优的 a，然后对π(s)做更新。

         对于值迭代和策略迭代很难说哪种方法好，哪种不好。对于规模比较小的马尔可夫决策过程来说，策略一般能够更快地收敛。但是对于规模很大（状态很多）的马尔可夫决策过程来说，值迭代比较容易。