机器学习笔记
本文作者:李德强
第二节 梯度下降
现有m个训练样本,每一个训练样本都有n个特征,那么我们对回归问题的数学期望为:

其中
我们为了确定 的值,我们需要让函数值减去样本值最小,即估计值最接近实际样本值:
的值,我们需要让函数值减去样本值最小,即估计值最接近实际样本值:

接下来使用梯度下降的方法来计算 的值:
的值:

我们对 求偏导数,即是梯度的方向,也就是
求偏导数,即是梯度的方向,也就是 值变化最快的方向。然后通过设定一个
值变化最快的方向。然后通过设定一个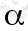 值来不断的迭代
值来不断的迭代 ,
,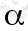 被称为是步长,如果
被称为是步长,如果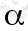 的值取的太小,则算法可能需要使用大量的时间算计才能够使
的值取的太小,则算法可能需要使用大量的时间算计才能够使 逐渐收敛,如果
逐渐收敛,如果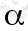 的值取的太大,算法可能会越过
的值取的太大,算法可能会越过 的最小值。所以
的最小值。所以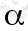 值的选择也是比较关键的。我们接下来看看对函数
值的选择也是比较关键的。我们接下来看看对函数 求偏导的过程:
求偏导的过程:

于是,我们有了对m个具有n个特征的训练样本的梯度下降算法:

此算法称为“批梯度下降算法”,对于训练样本数目比较大的时候算法的耗时通常也很大,于是我们进而使用“随机梯度下降算法”:

“随机梯度下降算法”的优点是可以在每次计算训练样本数据时即可对 的值进行更新,从而使
的值进行更新,从而使 能更快的趋于收敛,但它很难得到更准确的值,这种算法只会在准确值的附近徘徊。
能更快的趋于收敛,但它很难得到更准确的值,这种算法只会在准确值的附近徘徊。
Copyright © 2015-2023 问渠网 辽ICP备15013245号