机器学习笔记

        在上一节中我们知道使用批梯度下降算法时计算量很大，参数收敛速度较慢，而使用随机梯度下降时，参数收敛速度快，但有可能参数一直在极值附近徘徊，不一定能够完全收敛。下面我们来看一下代码的实现：

//求绝对值函数
double gabs(double x)
{
	if (x < 0)
	{
		return -x;
	}
	return x;
}

//h函数h(x) = theta0 * x0 + theta1 * x1 + ... + thetan * xn
double h(int feature_count, double *x, double *theta)
{
	double hval = 0;
	//累加求和
	for (int i = 0; i < feature_count; i++)
	{
		//设x0等于1
		if (i == 0)
		{
			hval = theta[i];
			continue;
		}
		//求累加和
		hval += theta[i] * x[i - 1];
	}
	return hval;
}

//随机梯度下降算法
void gradient_random(s_Sample *sample, double *theta)
{
	//alpha步长值为0.000001
	double alpha = 1e-6;
	//theta参数
	double *theta_t = malloc(sizeof(double) * sample->countf);
	//theta是否已收敛状态
	double *st = malloc(sizeof(int) * sample->countf);

	for (int i = 0; i < sample->countf; i++)
	{
		theta_t[i] = 999;
		st[i] = 1;
	}
	int t = 0;

	while (1)
	{
		int status = 0;
		for (int i = 0; i < sample->countf; i++)
		{
			//累加所有特征参数状态
			status += st[i];
			//如果已收敛则状态为0
			if (gabs(theta_t[i] - theta[i]) < (double) 1e-8 || theta_t[i] == theta[i])
			{
				st[i] = 0;
				break;
			}
			//遍历所有样本进行收敛计算
			for (int j = 0; j < sample->countx; j++)
			{
				theta_t[i] = theta[i];
				//设x0的值为1
				double x_i = 1;
				if (i > 0)
				{
					x_i = sample->x[j * sample->countf + (i - 1)];
				}
				double y_i = sample->x[j * sample->countf + (sample->countf - 1)];
				//随机梯度下降
				theta[i] -= alpha * (h(sample->countf, sample->x + j * sample->countf, theta) - y_i) * x_i;
			}
		}
		//所有theta参数收敛后跳出循环
		if (status == 0)
		{
			break;
		}
	}
}

        我们再来看一下100个训练样本：

1.000000, 15.150000
3.000000, 14.850000
3.000000, 20.850000
12.000000, 26.000000
5.000000, 15.550000
11.000000, 17.650000
11.000000, 25.650000
10.000000, 20.300000
15.000000, 20.050000
12.000000, 19.000000
17.000000, 22.750000
12.000000, 21.000000
19.000000, 29.450000
17.000000, 21.750000
21.000000, 26.150000
24.000000, 30.200000
25.000000, 31.550000
26.000000, 30.900000
25.000000, 31.550000
28.000000, 31.600000
30.000000, 27.300000
22.000000, 26.500000
26.000000, 24.900000
24.000000, 22.200000
31.000000, 28.650000
29.000000, 25.950000
34.000000, 28.700000
35.000000, 29.050000
33.000000, 28.350000
35.000000, 26.050000
39.000000, 32.450000
40.000000, 36.800000
38.000000, 34.100000
43.000000, 31.850000
41.000000, 36.150000
39.000000, 34.450000
40.000000, 30.800000
43.000000, 35.850000
44.000000, 34.200000
49.000000, 31.950000
41.000000, 30.150000
48.000000, 37.600000
48.000000, 35.600000
47.000000, 30.250000
53.000000, 32.350000
46.000000, 38.900000
53.000000, 33.350000
56.000000, 36.400000
57.000000, 40.750000
56.000000, 39.400000
58.000000, 43.100000
57.000000, 34.750000
57.000000, 33.750000
62.000000, 44.500000
61.000000, 42.150000
59.000000, 40.450000
66.000000, 37.900000
63.000000, 41.850000
67.000000, 45.250000
68.000000, 44.600000
62.000000, 44.500000
70.000000, 45.300000
65.000000, 44.550000
64.000000, 38.200000
72.000000, 47.000000
74.000000, 44.700000
74.000000, 42.700000
74.000000, 42.700000
73.000000, 45.350000
72.000000, 41.000000
76.000000, 47.400000
72.000000, 45.000000
73.000000, 44.350000
76.000000, 49.400000
79.000000, 42.450000
84.000000, 48.200000
79.000000, 47.450000
82.000000, 46.500000
85.000000, 47.550000
86.000000, 46.900000
83.000000, 48.850000
90.000000, 46.300000
84.000000, 49.200000
88.000000, 51.600000
87.000000, 52.250000
95.000000, 56.050000
95.000000, 56.050000
93.000000, 54.350000
94.000000, 46.700000
99.000000, 49.450000
92.000000, 53.000000
100.000000, 53.800000
98.000000, 50.100000
95.000000, 48.050000
103.000000, 58.850000
101.000000, 51.150000
102.000000, 54.500000
103.000000, 57.850000
101.000000, 50.150000
106.000000, 56.900000

        程序运行结果：

16.285443
0.383250

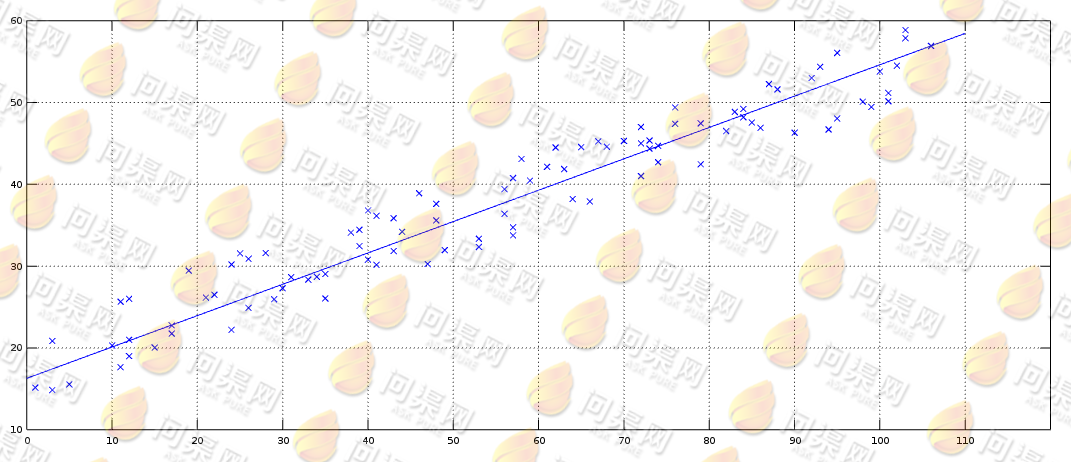
        最后使用图形方式来验证一下随机梯度下降算法：