机器学习笔记

        K-Mean与K值邻近类似，是通过样本与目标点的距离来做分类。但区别是K-Mean是一种典型的非监督学习算法，也就是说我们的数据是没有确定分类的，我们需要通过聚类算法将数据分类。即：将一部分数据聚成一类，将另外一些数据聚成另一类。例如，对于这样的数据分布：

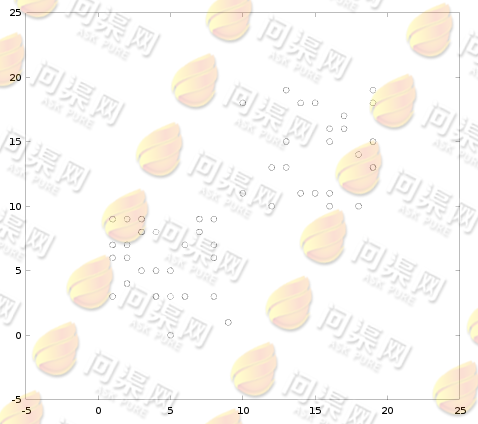
        通过我们人类的认知，我们可以对数据这样进行分类：

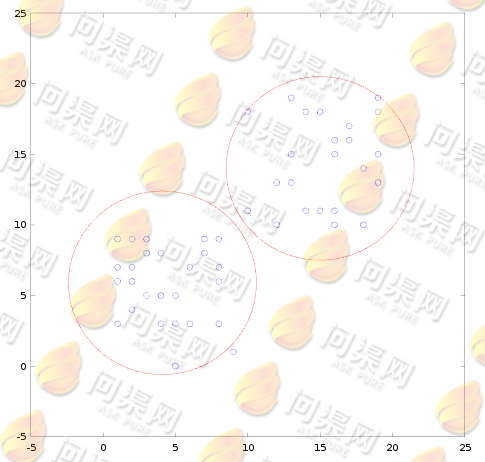
        即：我们将靠在一起的数据分为一组。

        K-Mean算法的思想是这样的，我们预计为数据分为两个类A和B，分别用红色和蓝色来表示。我们在样本的特征空间上任选2个点做为这两个分类的“质心”。然后分别计算数据到这两个质心的距离，到哪一个质心的距离最小，则认为此数据属于此分类。然后根据数据的新分类再重新计算2个分类的质心位置，不断重复计算质心的位置，直到质心全部收敛。

        正面我们用图形来看一下K-Mean算法的思想：首先在特征空间上任选2个点做为2个分类的质点（0, 20）和（20, 0）：

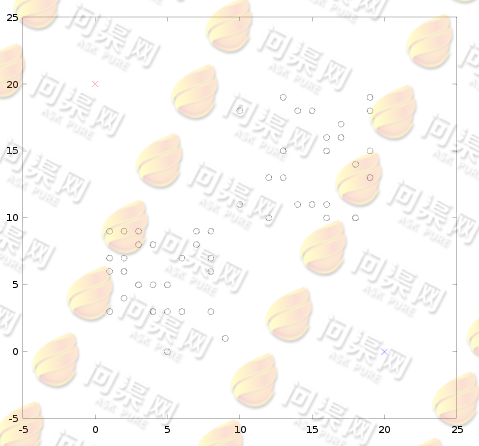
        然后根据这2个质心来计算数据与质心的距离，距哪一个质心近则属于哪一个分类，计算结果如下（红色为A类，蓝色为B类）：

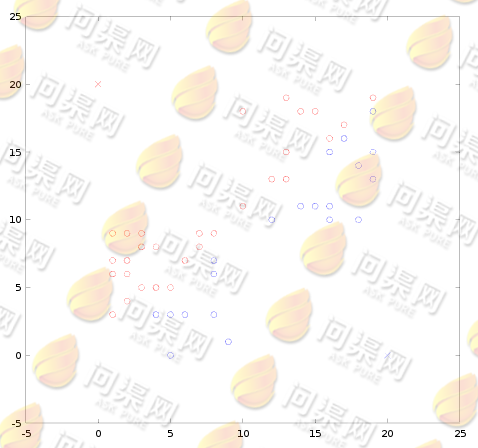
        再根据新分类数据计算出新的质心位置（7.7, 10.7）（12.6, 8.9），然后重复计算所有数据在新质点中的距离，并做出分类：

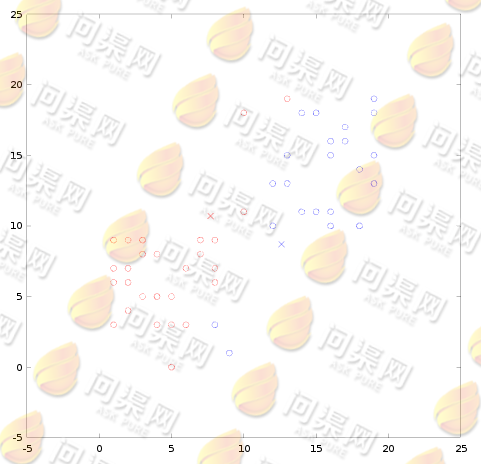
        重复计算质心位置与数据的分类（4.9, 7.4）（15.3, 13.1），直到质心位置收敛：

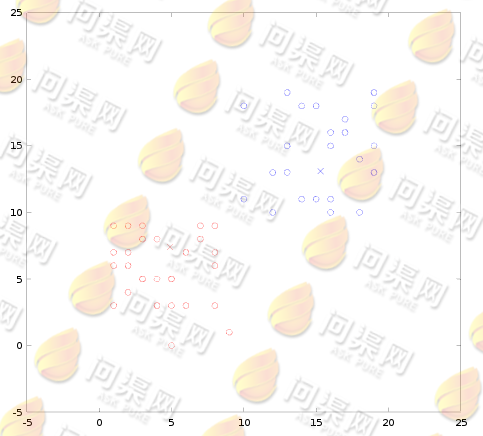
        得到质心收敛结果（4.2, 6.0）（15.0, 14.0）：

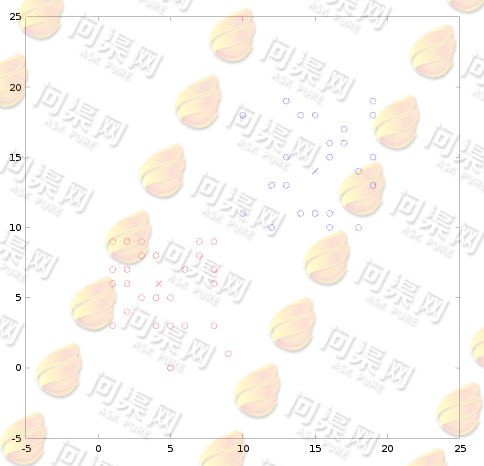
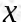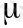        在聚类问题中我们的样本数据的特征依然是n维的，只是没有了y值，我们设样本为，设质心为，计算样本与质心距离的公式如下：

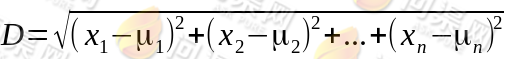
        由于算法的目标为找到样本与所以质心距离最小的那一个质心，所以，为了方便计算我们在计算距离时可以将开平方运算去掉（因为每一个距离都是开平方），所以比较距离大小的参考值为：

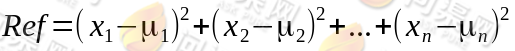
        具体的算法描述为：

        1.随机选取k个分类的质心，分别为。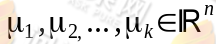

        2.对于每一个样本数据x，计算x到所有质心的距离，得到最小距离的质心，确定x所在的分类:

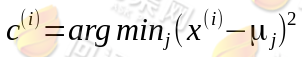
        3.对于每一个分类，均需要重新计算其质心：

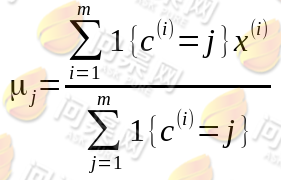
        4.确认质心与上一次计算的质心是否收敛？结束分类：跳转到第2步。