机器学习笔记
本文作者:李德强
第三节 对偶问题
回顾一下上一节中我们的目标函数:
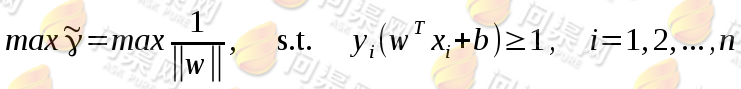
求解分数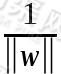 的最大值,其实就是求分母
的最大值,其实就是求分母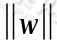 的最小值,为了方便后续求导计算,我们给
的最小值,为了方便后续求导计算,我们给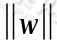 做平方除2,即:求
做平方除2,即:求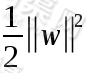 的最小值。于是目标由求最大值max问题变为求最小值的min问题,目标函数也变为:
的最小值。于是目标由求最大值max问题变为求最小值的min问题,目标函数也变为:
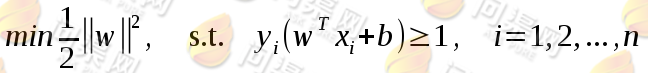
由于这个问题的特殊结构,还可以通过拉格朗日对偶性变换到对偶变量的优化问题,即通过求解与原问题等价的对偶问题得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:一者对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。拉格朗日对偶性是通过给每一个约束条件加上一个拉格朗日乘子α,定义拉格朗日函数:
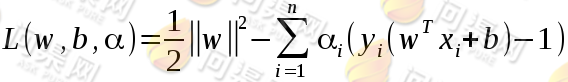
通过拉格朗日函数将约束条件融合到目标函数里去,从而只用一个函数表达式便能清楚的表达出我们的问题。设:
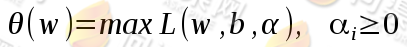
为了求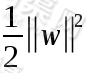 的最小值,其实就是求
的最小值,其实就是求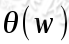 的最小值,于是有:
的最小值,于是有:
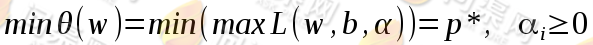
这里用p*来表示问题的最优值,等价于最初问题。为了方便计算,将min和max的计算顺序互换:
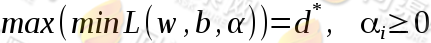
于是问题由p*变为d*并且有d* ≤ p*,在满足某些条件的情况下,这两者相等,这个时候就可以通过求解对偶问题来间接地求解原始问题。我们可能先求L对 w、b的极小,再求L对α的极大。
Copyright © 2015-2023 问渠网 辽ICP备15013245号