机器学习笔记

        当一个系统或过程在时刻t0所处的状态为已知的条件下，过程在时刻t > t0所处状态的条件分布与过程在时刻t0之前所处的状态无关.通俗地说，说是在已经知道过程“现在”的条件下，其“将来”不依赖于“过去”。

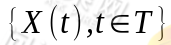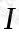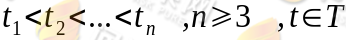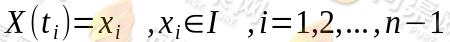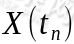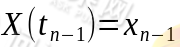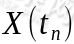        设随机过程的状态空间为，如果对时间t的任意n个数值在条件下，的条件分布函数恰等于在条件下的条件分布函数：

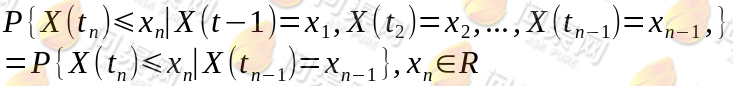
        或：

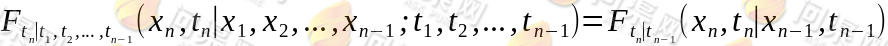
        则称过程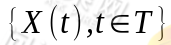具有马尔可夫性或无后效性，并称此过程为马尔可夫过程。

        泊松过程是时间连续状态离散的马尔可夫过程；维纳过程是时间状态都连续的马尔可夫过程。时间和状态都是离散的马尔可夫过程称为马尔可夫链，简称马氏链，记为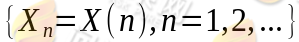，它可以看作在时间集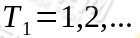上对离散状态的马氏过程观察的结果，我们约定记链的状态空间为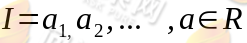，在链的情形，马尔可夫性通常用条件分布律来表示，即对任意的正整数n，r和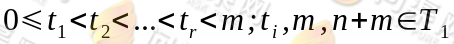有：

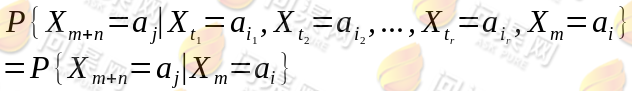
        其中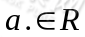记上式右端为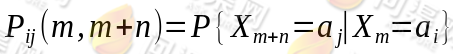，我们称条件概率

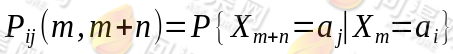
        为马氏链在时刻m处于状态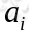条件下，在时刻m+n转移到状态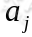的转移状态概率。由于链在时刻m从任务一个状态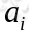出发到另一个时刻m+n，必然转移到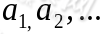诸多状态中的某一个，所以：

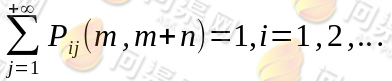
        由转移概率组成的矩阵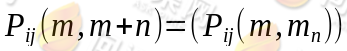称为马氏链的转移概率矩阵，此辞职的每一行元之和等于1。