机器学习笔记

        与线性回归的算法一样，不过由梯度下降改为梯度上升，函数由线性函数修改为Logistic函数：

//z = theta0 * x0 + theta1 * x1 + ... + thetan * xn
double h(int feature_count, double *x, double *theta)
{
	double z = 0.0;
	for (int i = 0; i < feature_count; i++)
	{
		z += theta[i] * x[i];
	}
	return 1.0 / (1.0 + pow(M_E, -z));
}

//随机梯度下降算法
void gradient_random(s_Sample *sample, double *theta)
{
	//alpha步长值为0.000001
	double alpha = 1e-5;
	//theta参数
	double *theta_t = malloc(sizeof(double) * sample->countf - 1);
	//theta是否已收敛状态
	double *st = malloc(sizeof(int) * sample->countf - 1);

	for (int i = 0; i < sample->countf - 1; i++)
	{
		theta_t[i] = 999;
		st[i] = 1;
	}
	int t = 0;

	while (1)
	{
		int status = 0;
		for (int i = 0; i < sample->countf - 1; i++)
		{
			//累加所有特征参数状态
			status += st[i];
			//如果已收敛则状态为0
			if (gabs(theta_t[i] - theta[i]) < (double) 1e-20 || theta_t[i] == theta[i])
			{
				st[i] = 0;
				break;
			}
			//遍历所有样本进行收敛计算
			for (int j = 0; j < sample->countx; j++)
			{
				theta_t[i] = theta[i];
				//设x0的值为1
				double x_i = sample->x[j * sample->countf + i];
				double y_i = sample->x[j * sample->countf + (sample->countf - 1)];
				//随机梯度上升
				theta[i] += alpha * (y_i - h(sample->countf, sample->x + j * sample->countf, theta)) * x_i;
			}
		}
		//所有theta参数收敛后跳出循环
		if (status == 0)
		{
			break;
		}
	}
}

        训练样本如下：

1,0,0
1,5,0
1,10,0
1,15,0
1,20,0
1,25,0
1,30,0
1,35,0
1,40,0
1,45,0
1,50,0
1,55,0
1,60,0
1,65,0
1,70,0
1,75,0
1,80,0
1,85,0
1,90,0
1,95,0
1,200,1
1,205,1
1,210,1
1,215,1
1,220,1
1,225,1
1,230,1
1,235,1
1,240,1
1,245,1
1,250,1
1,255,1
1,260,1
1,265,1
1,270,1
1,275,1
1,280,1
1,285,1
1,290,1
1,295,1
1,300,1
1,305,1
1,310,1
1,315,1
1,320,1
1,325,1
1,330,1
1,335,1
1,340,1
1,345,1
1,350,1
1,355,1
1,360,1
1,365,1
1,370,1
1,375,1
1,380,1
1,385,1
1,390,1
1,395,1
1,400,1
1,405,1
1,410,1
1,415,1
1,420,1
1,425,1
1,430,1
1,435,1
1,440,1
1,445,1
1,450,1
1,455,1
1,460,1
1,465,1
1,470,1
1,475,1
1,480,1
1,485,1
1,490,1
1,495,1

        程序运行结果：

-9.112109
0.065165

        最后来看一下Logistic回归的图形：

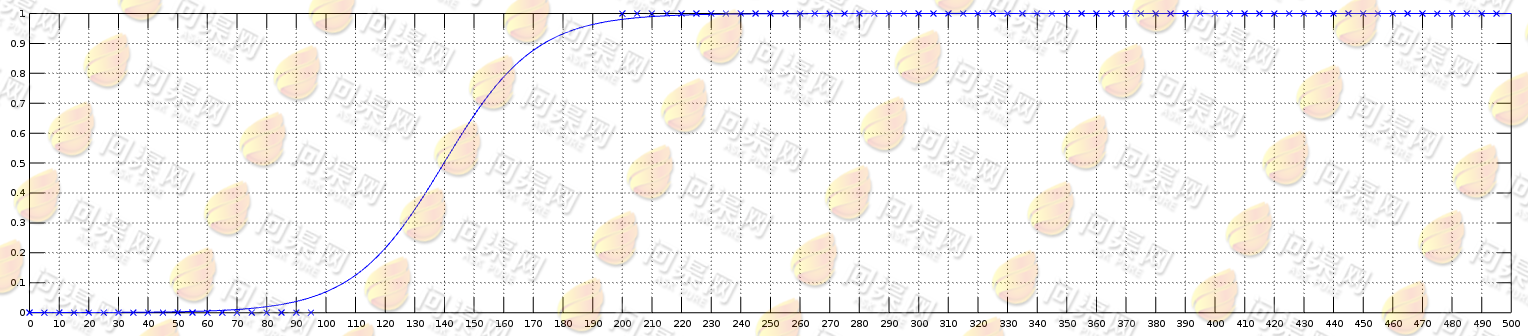
        对于这样的二值分类问题使用Logistic回归通常会是非常好的选择。