机器学习笔记
支持向量机被称作是最优分类器,它可以将我们的数据以“最优”的方式来分类。例如我们有两种不种的数据,分别是“x”和“o”如下图:
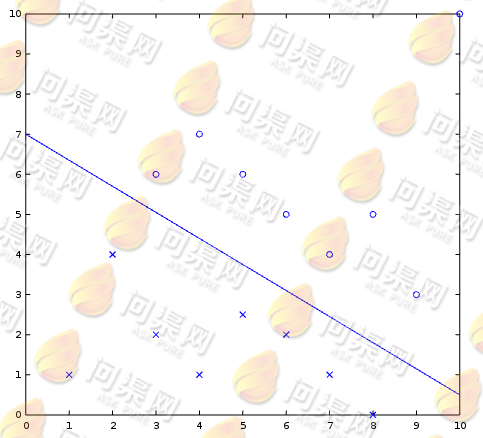
支持向量机的核心思想是在N维数据中找到一个超平面,使得这个超平衡可以完美的将数据进行分类(如上图中的直线将"x"类型数据和"o"类型数据划分开来,这两类数据刚好处于直线的两侧)。而这个超平面的函数为:
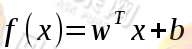
当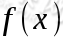 的值为0是表示在超平面上的点,而
的值为0是表示在超平面上的点,而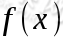 大于0的点对应y=1,而
大于0的点对应y=1,而 小于0的点对应y=-1如下图:
小于0的点对应y=-1如下图:
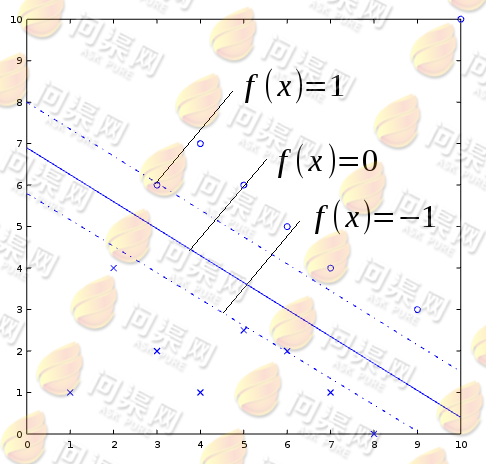
使用支持向量机对数据分类时数据的分类取值为-1和1,即二类问题。而当我们通过训练数据计算出了w和b的值之后就可以通过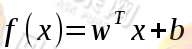 函数对指定的x来做分类预测,如果
函数对指定的x来做分类预测,如果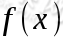 大于0则属于y=1类,如果
大于0则属于y=1类,如果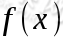 于小0则属于y=-1类。由于支持向量机使用超平面来分类数据,那么位于超平面两侧的数据符号就刚好相反,所以对于目标预测只需判断其符号即可。
于小0则属于y=-1类。由于支持向量机使用超平面来分类数据,那么位于超平面两侧的数据符号就刚好相反,所以对于目标预测只需判断其符号即可。
我们假定已经确定了超平面函数为: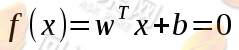 ,那么点到超平面的远近就可以使用
,那么点到超平面的远近就可以使用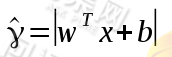 来表示。由于y的取值只有-1和1,而我们可以通过
来表示。由于y的取值只有-1和1,而我们可以通过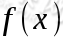 的符号来确定x的分类,于是我们就可以使用
的符号来确定x的分类,于是我们就可以使用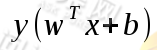 的符号来判断结果的正确性,于是函数间隔为:
的符号来判断结果的正确性,于是函数间隔为:
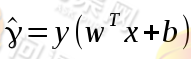
但是这样表示还是有问题的,为了能够找到这个超平面,我们希望两类训练样本到这个超平面的距离最大,这样才能很好的将数据分开,但使点到超平面的距离最大化可以通过等比例修改w和b的值做到,例如将w和b都修改成原来的2倍、4倍或n倍,所以使用函数间隔来确定超平面是无法做到的,所以需要引出另一个定义——几何间隔(geometrical margin):假定有一点x其在超平面上的垂直投影为x0,而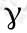 是点x到超平面的距离,w为垂直于超平面的一个向量,如下图:
是点x到超平面的距离,w为垂直于超平面的一个向量,如下图:
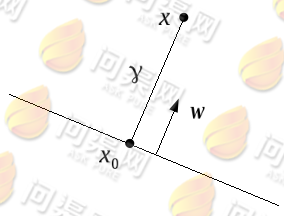
于是x为:
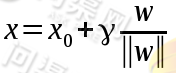
由于x0是在超平面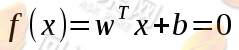 上的点,将x0代入
上的点,将x0代入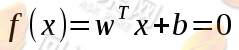 得到点x到超平面的距离为:
得到点x到超平面的距离为:
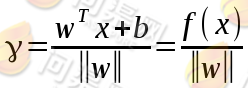
由于y取值与x位于超平面的位置有关,为了得到其取值的绝对值,点x到超平面的几何间隔定义为:
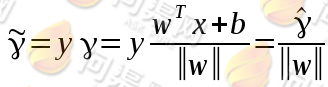
Copyright © 2015-2023 问渠网 辽ICP备15013245号