机器学习笔记
在上一节我们学习了对于线性不可分情况的解决办法是将数据由低维度特征空间映射到高维度特征空间,也就是说将非线性特征集映到另一个高维度的线性特征集,也就是说要将数据加入一个新的计算函数,这等价于将数据映射到一个更高维度的空间。我们定义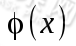 是将x从原特征空间映射到另一个特征空间的函数,于是我们的超平面函数就变为:
是将x从原特征空间映射到另一个特征空间的函数,于是我们的超平面函数就变为:
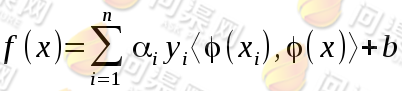
我们可以通过在特征空间中直接计算内积 来计算数据分类,通过这种方式被称为“核函数计算方法”。而函数
来计算数据分类,通过这种方式被称为“核函数计算方法”。而函数 称为“核函数”。让我们再回到上一节的线性不可分的问题来学习“核函数”的真正意义。再来看一下我们的训练数据:
称为“核函数”。让我们再回到上一节的线性不可分的问题来学习“核函数”的真正意义。再来看一下我们的训练数据:
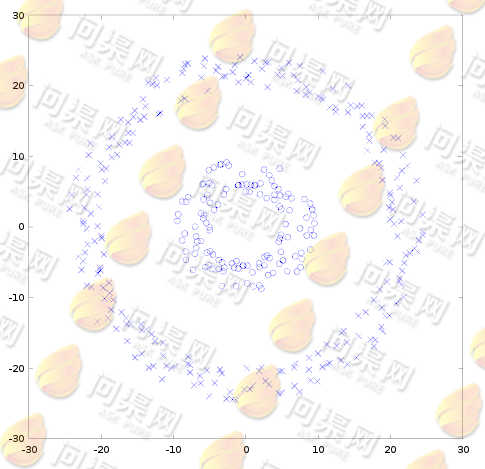
在前面我们学习过对线性不可分的解决 办法,我们可以将这个二维空间的数据映射到三维空间中。但我们通过直观的分析会发现使用一个二维的二次曲线即可以完美的将这样的数据划分为两个区域而不是一个在三维空间中的一个二维超平面:
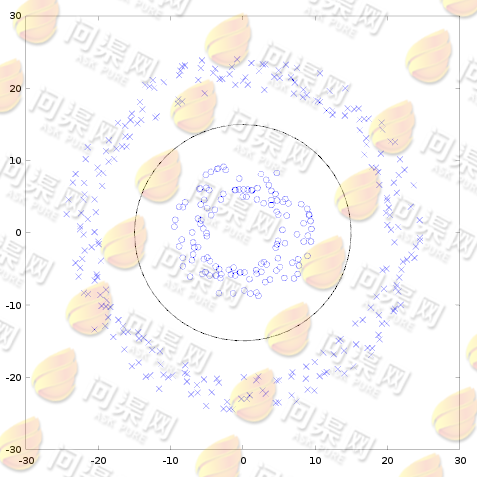
于是我们想到在N维空间中我们是否可以使用N维的曲线来为数据进行分类来划分呢?我们知道一条二次曲线(圆是二次曲线的一种特殊情形)的方程可以写成这样的形式:

如果我们把这个式子写成向量的形式:

即:
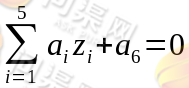
于是,我们构造出了一个五维空间,在这个五维空间中数据就变为了线性可分的。从而将线性不可分的数据在高维度空间中变成线性可分的,这也就是kernel核函数的基本思想。核函数相当于把原来的分类函数:
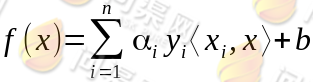
映射成:
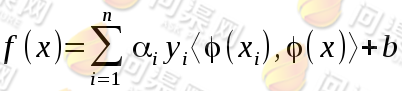
然而这样解决分类问题的过程会给计算带来更大的困难,我们用二维数据的例子向高维度空间做映射,得到的是一个五维空间,如果我们的原始数据是三个维度的话,如果再向高维度映射,得到是三个维度的变量的一次和二次的组合即十九维度空间,这样的高维度给我们的计算带来更大的难度,甚至在原始维度更高时映射空间就会程爆炸性增长,导致计算会越来越困难甚至是无法计算。正面我们来看这样一个核函数:

经过计算我们发现计算原始特征x和z内积的平方,其结果等价于映射后特征的内积。再来看另外一个核函数:
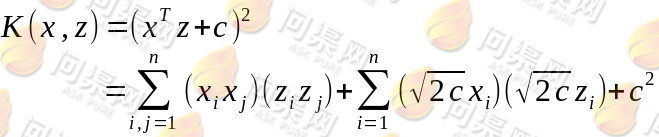
一般的,多项式核函数为:
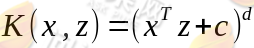
这个核函数所映射出的空间维度是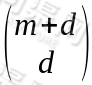 ,其中m为原始空间维度。
,其中m为原始空间维度。
核函数引入能从计算上方便我们求向量的内积,也就是简化向量内积的计算过程。现在我们的分类函数可以写成核函数的形式:
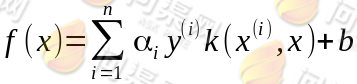
其中k即为核函数kernel(x, z),而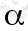 可以通过下面条件计算:
可以通过下面条件计算:
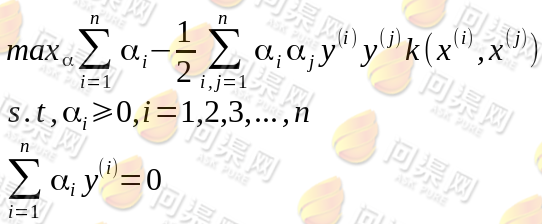
下面我们来看几个常用的核函数:
- 多项式核:
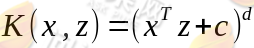 即上述例子中的核函数
即上述例子中的核函数 - 高斯核:
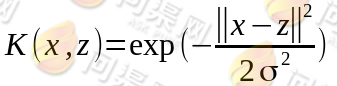 如果x和z很相近,那么核函数值为1,如果x和z相差很大,那么核函数值约等于0。由于这个函数类似于高斯分布,因此称为高斯核函数,也叫做径向基函数。它能够把原始特征映射到无穷维。
如果x和z很相近,那么核函数值为1,如果x和z相差很大,那么核函数值约等于0。由于这个函数类似于高斯分布,因此称为高斯核函数,也叫做径向基函数。它能够把原始特征映射到无穷维。 - 线性核:
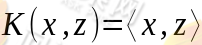 这实际上就是原始空间中的内积。
这实际上就是原始空间中的内积。
Copyright © 2015-2023 问渠网 辽ICP备15013245号