机器学习笔记

        在本节我们来一起学习马尔可夫决策过程。一个马尔可夫决策过程由一个五元组构成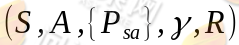

• S表示状态集(states)。
• A表示一组动作(actions)。
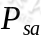• 表示状态转移概率，它所表示的是在当前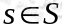状态下，经过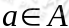的作用后，会转移到其他状态的概率分布情况（当前状态执行a后可能跳转到很多状态）。
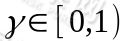• 是阻尼系数(discount factor)。
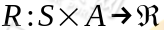• ，R是回报函数(reward function)回报函数经常写作 S 的函数(只与 S有关),这样的话,R 重新写作。

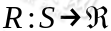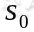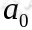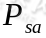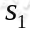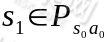        马尔可夫决策过程如下：某个 agent 的初始状态为，然后从 A 中挑选一个动作执行，执行后agent 按概率随机转移到了下一个状态。然后再执行一个动作，
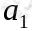就转移到了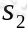，接下来再执行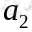，我们可以用下面的图表示整个过程：

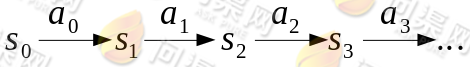
        在定义了转移路径之后，得到的回报函数之和如下：

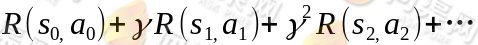
        如果R只和S有关,那么上式可以写作：

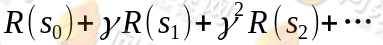
        我们的目标是选择一组最佳的 action,使得全部的回报加权和期望最大：

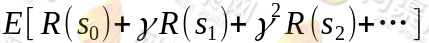
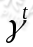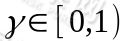        从上式可以发现，在 t 时刻的回报值已经变为了，由于所以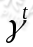在经过时间流失后不断衰减的过程，越靠后的状态对回报和影响越小。最大化期望值也就是要将大的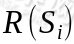尽量放到前面，小的尽量放到后面。已经处于某个状态s时，我们会以一定策略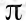来选择下一个动作a执行，然后转换到另一个状态s'。我们将这个动作的选择过程称为策略(policy),每一个策略其实就是一个状态到动作的映射函数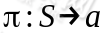。给定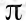也就给定了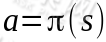，也就是说，知道了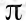就知道了每个状态下一步应该执行的动作。我们为了区分不同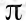的好坏，并定义在当前状态下，执行某个策略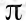后，出现的结果的好坏，需要定义值函数(value function)也叫折算累积回报(discounted cumulative reward)

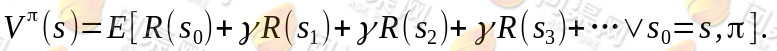
        可以看到，在当前状态s下，选择好策略后,值函数是回报加权和期望。给定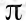也就给定了一条未来的行动方案，这个行动方案会经过一个个的状态，而到达每个状态都会有一定回报值，距离当前状态越近的其他状态对方案的影响越大，权重越高。这和下象棋差不多，在当前棋局s0下，不同的走子方案是，我们评价每个方案依靠对未来局势(R(s 1 ), R(s 2 ),...)的判断。一般情况下,我们会在头脑中多考虑几步，但是我们会更看重下一步的局势。从递推的角度上考虑，当期状态s的值函数 V,其实可以看作是当前状态的回报 R(s)和下一状态的值函数 V’之和,也就是将上式变为：

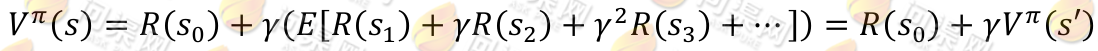
        然而，我们需要注意的是虽然给定π后,在给定状态s下，a 是唯一的，但A ⟼ S可能不是多到一的映射。由Bellman等式，从上式得到：

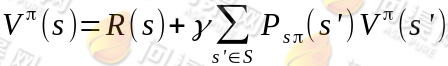
        其中s'表示下一个状态，当状态个数有限时，我们可以通过上式来求出每一个 s 的V(终结状态没有第二项 V(s’))。如果列出线性方程组的话，也就是|S|个方程，|S|个未知数，直接求解即可。当然，我们求V的目的就是想找到一个当前状态s下，最优的行动策略π，定义最优的V*如下：

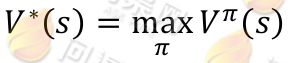
        就是从可选的策略π中挑选一个最优的策略(discounted rewards 最大)。上式的 Bellman 等式形式如下：

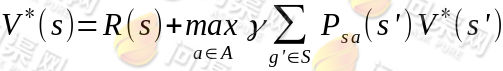
        第一项与π无关，所以不变。第二项是一个π就决定了每个状态s的下一步动作a，执行a后，s’按概率分布的回报概率和的期望。定义了最优的 V*，我们再定义最优的策略π*: S⟼A如下：

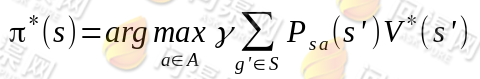
        选择最优的π* ，也就确定了每个状态s的下一步最优动作a。根据以上式子，我们可以知道：

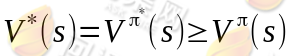
        就是当前状态的最优的值函数V*，是由采用最优执行策略π*的情况下得出的，采用最优执行方案的回报显然要比采用其他的执行策略π要好。这里需要注意的是，如果我们能够求得每个s下最优的a，那么从全局来看S⟼A的映射即可生成，而生成的这个映射是最优映射，称为π*。π*针对全局的s确定了每一个s的下一个行动a，不会因为初始状态s选取的不同而不同。