机器学习笔记

        我们在使用支持向量机对数据进行分类时，是以数据到超平衡的距离为依据的，数据点距离超平面的距离越大，用于分类的超平面就越可信。在上一节我们分析了一个问题，就是假设w和b同时变为原来的2倍、4倍或n倍时，所有的点到这个超平面的距离都变大了，但这样的超平面有无数多个，并且不是我们要的可分类的超平面。所以我们引出“几何间隔”的定义，几何间隔的计算是函数间隔除以w的二阶范数。使用几何间隔的好处是在缩放w和b的值是几何间隔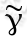不变。也就是说几何间隔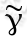不会随w和b的缩放而变化，只有在超平面的方向和位置变化时几何间隔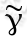才会发生变化。于是使用几何间隔来测量点到超平面的距离就比较合理。几何间隔即为下图中两条虚线间隔的一半，也就是虚线到实线（超平面）的间隔：

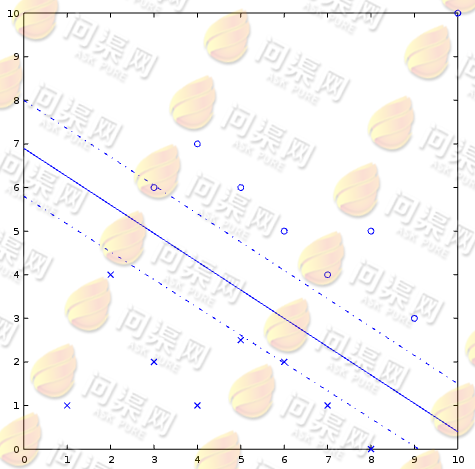
        于是最大间隔分类器的目标函数可以定义为：

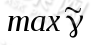
        由几何间隔的定义可知：

        即训练样本到超平面的几何间隔为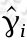，这些样本点到超平面的几何间隔就应该大于等于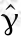，并由几何间隔的定义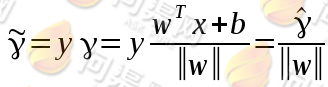可知，若将函数间隔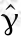设为1，则有：

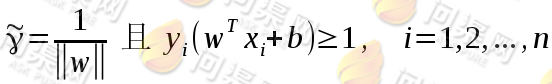
        于是目标函数转化为：

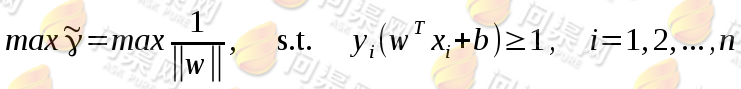
        在这个式子中“s.t.”表示为“subject to”。

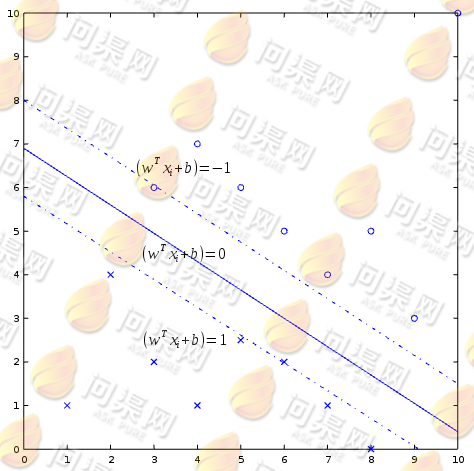
        如上图所示，我们根据训练样本找到的一个超平面为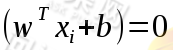，而落在虚线上的点则被称为支持向量。