机器学习笔记
K值邻近分类算法是机器学习中最简单的算法之一,它的思想为将给定目标样本与所有训练样本做距离计算,并将结果按升序排列。对目标样本分类的过程也非常简单,即:找出给距离最小的前n个值中同类最多的分类即是目标样本的所属分类。具体来说,比如我们有10个房屋的训练样本,其中的3表分别为“价格”/“面积”/“合理”。样本如下:
| 价格 | 面积 | 是否合理 |
| 45 | 40 | 1 |
| 79 | 54 | 0 |
| 99 | 118 | 0 |
| 48 | 45 | 1 |
| 69 | 78 | 1 |
| 87 | 83 | 0 |
| 68 | 76 | 1 |
| 80 | 76 | 0 |
| 88 | 102 | 1 |
| 60 | 49 | 0 |
我们首先用可视化的方式来看看这些样本,其中O表示“合理”而X表示“不合理”:
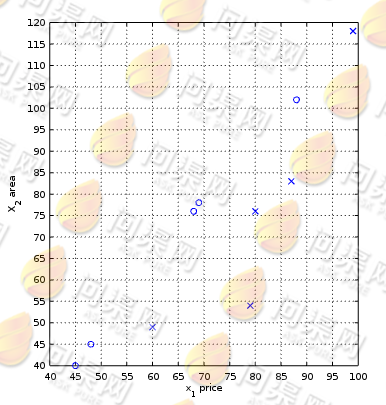
现在我们有一个新的样本需要分类:63万、74平方米,即:x1 = 49, x2 = 50 于是需要我们通过算法来预测这两个特征所属的分类,即“合理”还是“不合理”。我们将目标样本与所有训练样本做距离计算,并找出最近的样本,如下图:
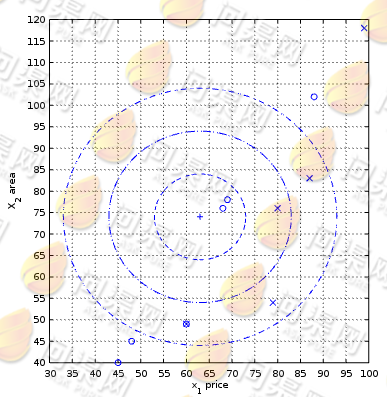
我们分别来看这3个尺度的圆,在第1个小圆中距离目标样本“+”最近的有2个训练样本分类均为“o”;在第2个圆中有3个训练样本分类为“oox”;在第3个大圆中有6个训练样本分类为“xxxxoo”。通过这个盒子我们可以看到在不同的距离范围下,距离分类的结果也不同。但通常的做法为取K个距离目标样本最近的值,并找出同一分类最多的值,在我们这个盒子中我们选定K的值为3,即在第2个圆中有2个o和1个x,所以我们认为样本(63, 74)的结果为1即“合理”。在实际使用过程中,我们的样本特征并不会只有两个,每一个样本通都会有多个特征。
另外,在对每一个特征做距离计算时,要对每一个特征值做范围归一处理。通俗来讲,就是将每一个特征的取值范围统一。例如在房价是否合理的问题中,房屋面积和价格的取值范围通常是不一至的,如果我们再加入一个新的特征,比如房间数。各个特征的取值范围就完全不同了,面积通常在30~200之间,价格也通常在30万~200万之间,房间数通常是1~5之间。如果不做范围统一,那么在距离计算时房间数这个特征对距离的影响就非常之小了,但在实际中这个特征也非常重要,所以我们通常要将所有特征的值转为统一的大小。做法如下:
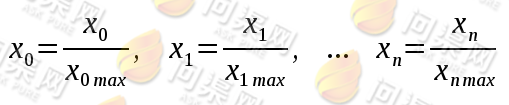
首先找出每一个特征的最大值,并在做距离计算时将每一个特征的值除以这个特征的最大值,结果会得到一个0~1之间的数,所以对每一个特征进行范围归一处理,得到的所有特征值都是范围统一的,每个特征对目标的影响都是相同的。
现在我们来看一看距离计算的公式,假设我们有i个训练样本,每一个训练样本的特征数为n,那么我们采用的欧式距离公式为:
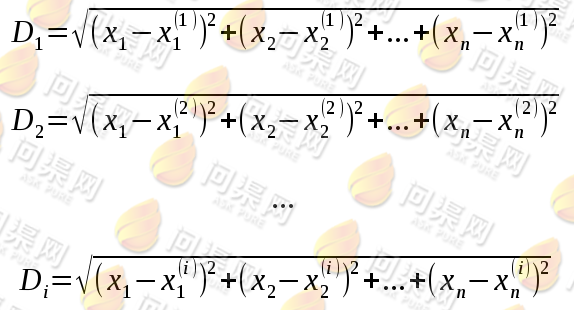
D表示与各个样本的距离,X表示目标样本的多个特征,X右上角的(i)表示第i个训练样本。计算出各个距离值并按升序排列之后即可对目标样本进行分类预测。
Copyright © 2015-2023 问渠网 辽ICP备15013245号