机器学习笔记
本文作者:李德强
第二节 独立成分分析
我们的问题已经阐述的很清晰了,我们希望能通过某方法将混合的声音样本将每一种分享开来,也就是说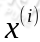 的每个分量都由
的每个分量都由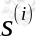 的分量线性表示。A和s都是未知的,但x是已知的,我们要想办法根据x来推出s,这个过程也称作为盲信号分离:
的分量线性表示。A和s都是未知的,但x是已知的,我们要想办法根据x来推出s,这个过程也称作为盲信号分离:
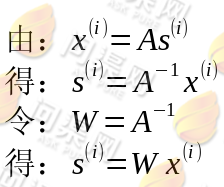
于是我们可以将W写成行向量的形式:
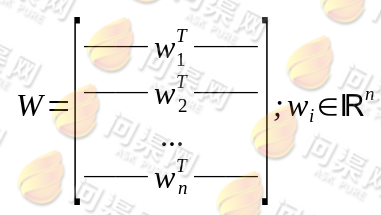
最后我们得到信号源:
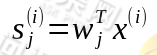
下面我们就来了解一下独立成分分析算法(Independent Component Analysis)。我们假设每一个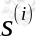 都有概率密度
都有概率密度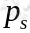 ,并且假设每个人发出的声音信号各自独立,那么给定时刻的原信号的联合分布为:
,并且假设每个人发出的声音信号各自独立,那么给定时刻的原信号的联合分布为:
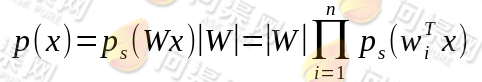
因为W和s都是未知的,所以无法直接求得W。在这里我们可以选取一个概率密度函数赋给s,但是不能选高斯分布密度函数。因为密度函数p(x)由累计分布函数F(x)求导得到。F(x)要满足单调递增并且值域在[0, 1]。这里我们选取sigmoid函数,它的定义域为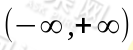 值域刚好在[0, 1]中。我们来一下它的函数原型:
值域刚好在[0, 1]中。我们来一下它的函数原型:
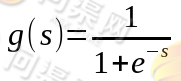
对g(s)求导得:
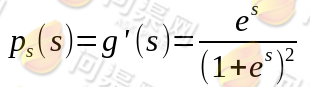
下面在给定了采样后的样本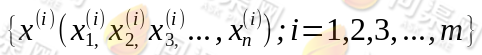 对数似然估计如下:
对数似然估计如下:
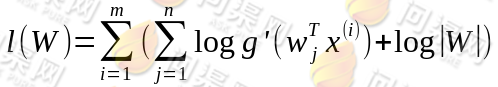
接下来我们需要对W求导,推导过程略,得到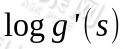 的导数为
的导数为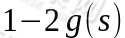 :
:
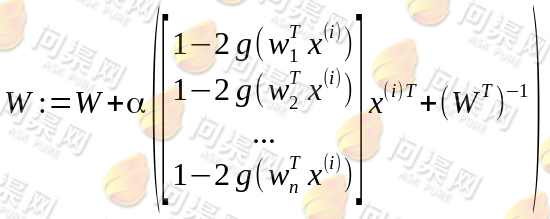
其中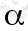 为梯度上升速率,当迭代出w后就可根据
为梯度上升速率,当迭代出w后就可根据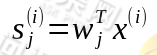 来得出原始信号了。
来得出原始信号了。
Copyright © 2015-2023 问渠网 辽ICP备15013245号