数据结构实战

        平衡二叉树又称AVL树。平衡二叉树的特性为：它的左子树和右子树都是平衡二叉树，并且左子树和右子树的深度差的绝对值不超过1。对二叉树插入新节点后，如果二叉树的左子树和右子树的深度差的绝对值超过1，则表示这个二叉树失去了平衡。于是我们就要对失衡的二叉树做“恢复平衡”的操作。对失衡的二叉树做平衡处理可以归纳为4种情况：

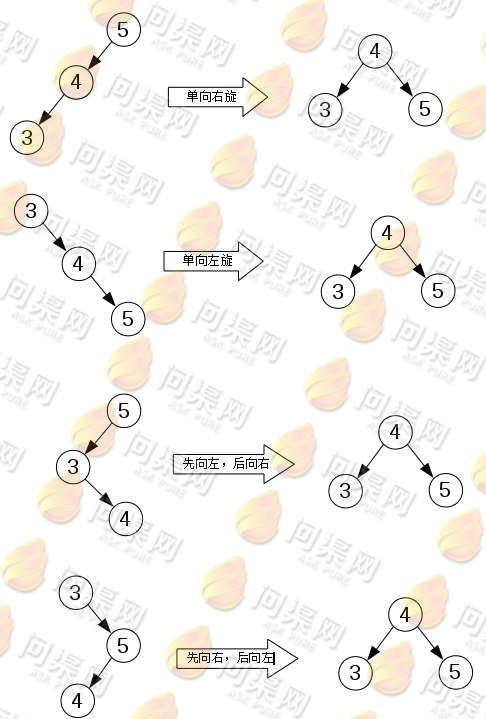
        首先修改二叉树的数据结构定义，加入两个新的变量分别用于存放以当前节点为根节点的子树的高度和平衡因子（左子树高度减去右子树高度）：

//关键字变量类型
typedef s32 tkey;

//二叉树节点
typedef struct s_tree_node
{
	//数据值
	void *value;
	//关键字
	tkey key;
	//平衡因子
	int bf;
	//节点高（深度）
	int height;
	//左孩子节点
	struct s_tree_node *left_child;
	//右孩子节点
	struct s_tree_node *right_child;

} s_tree_node;

//平衡二叉树
typedef struct s_avl_tree
{
	//根节点
	s_tree_node *root;
} s_avl_tree;

        再来实现平衡二叉树的插入操作，并实现“恢复平衡”的操作：

int avl_tree_insert(s_tree_node **node, tkey key, void *value)
{
	if (node == NULL)
	{
		return -1;
	}

	if (*node == NULL)
	{
		//创建新节点
		s_tree_node *p_new = (s_tree_node *) malloc(sizeof(s_tree_node));
		if (p_new == NULL)
		{
			//printf("[ERROR] Alloc memory failed!\n");
			return -1;
		}
		p_new->key = key;
		p_new->value = value;
		p_new->bf = 0;
		p_new->height = 0;
		p_new->left_child = NULL;
		p_new->right_child = NULL;
		*node = p_new;

		return 0;
	}

	//找到相同的关键字
	if (key == (*node)->key)
	{
		//printf("[ERROR] Find the same key \"%d\"!\n", key);
		return -1;
	}

	//如果关键字小，在其左子树上处理
	if (key < (*node)->key)
	{
		int st = avl_tree_insert(&(*node)->left_child, key, value);
		//平衡处理
		avl_tree_rebalance(node);
		return st;
	}

	//如果关键字大，在其右子树上处理
	int st = avl_tree_insert(&(*node)->right_child, key, value);
	//平衡处理
	avl_tree_rebalance(node);
	return st;
}

//删除关键字节点
int avl_tree_delete(s_tree_node **node, tkey key)
{
	if (node == NULL)
	{
		return -1;
	}

	if (*node == NULL)
	{
		return -1;
	}

	//找到关键字相同的节点
	if (key == (*node)->key)
	{
		//删除此节点
		return avl_tree_delete_node(node);
	}
	//如果小于当前节点，则在其左子树上处理
	if (key < (*node)->key)
	{
		int st = avl_tree_delete(&(*node)->left_child, key);
		//平衡处理
		avl_tree_rebalance(node);
		return st;
	}

	//如果大于当前节点，则在其右子树上处理
	int st = avl_tree_delete(&(*node)->right_child, key);
	//平衡处理
	avl_tree_rebalance(node);
	return st;
}

//删除节点
int avl_tree_delete_node(s_tree_node **node)
{
	if (node == NULL)
	{
		return -1;
	}

	if (*node == NULL)
	{
		return -1;
	}

	//如果是叶子节点
	if ((*node)->left_child == NULL && (*node)->right_child == NULL)
	{
		s_tree_node *p_del = *node;
		*node = NULL;
		free(p_del);
		return 0;
	}

	//如果只有左子树
	if ((*node)->left_child != NULL && (*node)->right_child == NULL)
	{
		s_tree_node *p_del = *node;
		*node = (*node)->left_child;
		free(p_del);
		return 0;
	}

	//如果只有右子树
	if ((*node)->left_child == NULL && (*node)->right_child != NULL)
	{
		s_tree_node *p_del = *node;
		*node = (*node)->right_child;
		free(p_del);
		return 0;
	}

	//如果平衡因子>=0说明左高右低
	if ((*node)->bf >= 0)
	{
		//找到node节点的左子树中权值最大的节点
		s_tree_node **p_del = avl_tree_find_max_node(&(*node)->left_child);
		avl_tree_node_swap(*node, *p_del);
		return avl_tree_delete_node(p_del);
	}

	//如果平衡因子<0说明左低右高
	//找到node节点的左子树中权值最小的节点
	s_tree_node **p_del = avl_tree_find_min_node(&(*node)->right_child);
	avl_tree_node_swap(*node, *p_del);
	return avl_tree_delete_node(p_del);
}

        接下来实现4种旋转操作：

//二叉树的平衡处理
void avl_tree_rebalance(s_tree_node **node)
{
	if (node == NULL)
	{
		return;
	}

	if (*node == NULL)
	{
		return;
	}

	//计算节点高（深度）
	(*node)->height = avl_tree_height(*node);
	//计算节点的平衡因子（左子树高减去右子树高）
	(*node)->bf = avl_tree_bf(*node);

	if ((*node)->bf > 1 && (*node)->left_child->right_child == NULL)
	{
		//单向右旋
		avl_tree_single_right(node);
		//对处理后的节点再做平衡处理
		avl_tree_rebalance(&(*node)->left_child);
		avl_tree_rebalance(&(*node)->right_child);
		avl_tree_rebalance(node);
		return;
	}

	if ((*node)->bf > 1 && (*node)->left_child->right_child != NULL)
	{
		//先左旋再右旋
		avl_tree_left_right(node);
		//对处理后的节点再做平衡处理
		avl_tree_rebalance(&(*node)->left_child);
		avl_tree_rebalance(&(*node)->right_child);
		avl_tree_rebalance(node);
		return;
	}

	if ((*node)->bf < -1 && (*node)->right_child->left_child == NULL)
	{
		//单向左旋
		avl_tree_single_left(node);
		avl_tree_rebalance(&(*node)->left_child);
		avl_tree_rebalance(&(*node)->right_child);
		//对处理后的节点再做平衡处理
		avl_tree_rebalance(node);
		return;
	}

	if ((*node)->bf < -1 && (*node)->right_child->left_child != NULL)
	{
		//先右旋再左旋
		avl_tree_right_left(node);
		avl_tree_rebalance(&(*node)->left_child);
		avl_tree_rebalance(&(*node)->right_child);
		//对处理后的节点再做平衡处理
		avl_tree_rebalance(node);
		return;
	}
}

//计算节点的高（深度）
int avl_tree_height(s_tree_node *node)
{
	if (node == NULL)
	{
		return -1;
	}
	//递归计算左子树高
	int height_left = avl_tree_height(node->left_child);
	//递归计算右子树高
	int height_right = avl_tree_height(node->right_child);
	//左右子树较大的一侧的高度加一
	return height_left > height_right ? height_left + 1 : height_right + 1;
}

//计算平衡因子，左子树高减去右子树高
int avl_tree_bf(s_tree_node *node)
{
	if (node == NULL)
	{
		return 0;
	}
	//左右子树为空
	if (node->left_child == NULL && node->right_child == NULL)
	{
		return 0;
	}
	//只有左子树
	if (node->left_child != NULL && node->right_child == NULL)
	{
		return node->height;
	}
	//只有右子树
	if (node->left_child == NULL && node->right_child != NULL)
	{
		return -(node->height);
	}
	//左子树高减去右子树高
	return node->left_child->height - node->right_child->height;
}

//单向右旋
void avl_tree_single_right(s_tree_node **node)
{
	s_tree_node **pA = node;
	s_tree_node **pB = &(*pA)->left_child;
	s_tree_node **pC = &(*pB)->right_child;

	s_tree_node *nA = *pA;
	s_tree_node *nB = *pB;
	s_tree_node *nC = *pC;

	//平衡旋转
	*pB = nC;
	*pC = nA;
	*pA = nB;

	//重新计算树高和平衡因子
	nA->height = avl_tree_height(nA);
	nB->height = avl_tree_height(nB);
	nA->bf = avl_tree_bf(nA);
	nB->bf = avl_tree_bf(nB);
}

//单向左旋
void avl_tree_single_left(s_tree_node **node)
{
	s_tree_node **pA = node;
	s_tree_node **pB = &(*pA)->right_child;
	s_tree_node **pC = &(*pB)->left_child;

	s_tree_node *nA = *pA;
	s_tree_node *nB = *pB;
	s_tree_node *nC = *pC;

	//平衡旋转
	*pB = nC;
	*pC = nA;
	*pA = nB;

	//重新计算树高和平衡因子
	nA->height = avl_tree_height(nA);
	nB->height = avl_tree_height(nB);
	nA->bf = avl_tree_bf(nA);
	nB->bf = avl_tree_bf(nB);
}

//先左旋再右旋
void avl_tree_left_right(s_tree_node **node)
{
	s_tree_node **pA = node;
	s_tree_node **pB = &(*pA)->left_child;
	s_tree_node **pC = &(*pB)->right_child;
	s_tree_node **pD = &(*pC)->left_child;
	s_tree_node **pE = &(*pC)->right_child;

	s_tree_node *nA = *pA;
	s_tree_node *nB = *pB;
	s_tree_node *nC = *pC;

	//平衡旋转
	*pC = nC->left_child;
	*pB = nC->right_child;
	*pD = nB;
	*pE = nA;
	*pA = nC;

	//重新计算树高和平衡因子
	nA->height = avl_tree_height(nA);
	nB->height = avl_tree_height(nB);
	nC->height = avl_tree_height(nC);
	nA->bf = avl_tree_bf(nA);
	nB->bf = avl_tree_bf(nB);
	nC->bf = avl_tree_bf(nC);
}

//先右旋再左旋
void avl_tree_right_left(s_tree_node **node)
{
	s_tree_node **pA = node;
	s_tree_node **pB = &(*pA)->right_child;
	s_tree_node **pC = &(*pB)->left_child;
	s_tree_node **pD = &(*pC)->left_child;
	s_tree_node **pE = &(*pC)->right_child;

	s_tree_node *nA = *pA;
	s_tree_node *nB = *pB;
	s_tree_node *nC = *pC;

	//平衡旋转
	*pB = nC->left_child;
	*pC = nC->right_child;
	*pD = nA;
	*pE = nB;
	*pA = nC;

	//重新计算树高和平衡因子
	nA->height = avl_tree_height(nA);
	nB->height = avl_tree_height(nB);
	nC->height = avl_tree_height(nC);
	nA->bf = avl_tree_bf(nA);
	nB->bf = avl_tree_bf(nB);
	nC->bf = avl_tree_bf(nC);
}

        最后写一个main函数来构建一个平衡二叉树：

#include <stdio.h>
#include <stdlib.h>
#include "tree.h"

int main(int argc, char **args)
{

	//初始化树
	s_tree tree;
	tree_init(&tree);

	tree_insert(&tree, 1);
	tree_insert(&tree, 3);
	tree_insert(&tree, 4);
	tree_insert(&tree, 6);
	tree_insert(&tree, 7);
	tree_insert(&tree, 2);
	tree_insert(&tree, 9);
	tree_insert(&tree, 8);
	tree_insert(&tree, 0);
	tree_insert(&tree, 5);

	//中序遍历
	tree_inorder_visit(&tree, tree.root);

	//销毁树
	tree_destroy(&tree);

	return 0;
}

        运行结果：

key: 0, value: -1, height: 0, bf: 0.
key: 1, value: -1, height: 1, bf: 1.
key: 2, value: -1, height: 2, bf: 1.
key: 3, value: -1, height: 0, bf: 0.
key: 4, value: -1, height: 3, bf: 0.
key: 5, value: -1, height: 0, bf: 0.
key: 6, value: -1, height: 2, bf: -1.
key: 7, value: -1, height: 0, bf: 0.
key: 8, value: -1, height: 1, bf: 0.
key: 9, value: -1, height: 0, bf: 0.

4
	2
		1
			0
		3
	6
		5
		8
			7
			9

        我们来看一下这个二叉树在“恢复平衡”操作前后的结果对比：

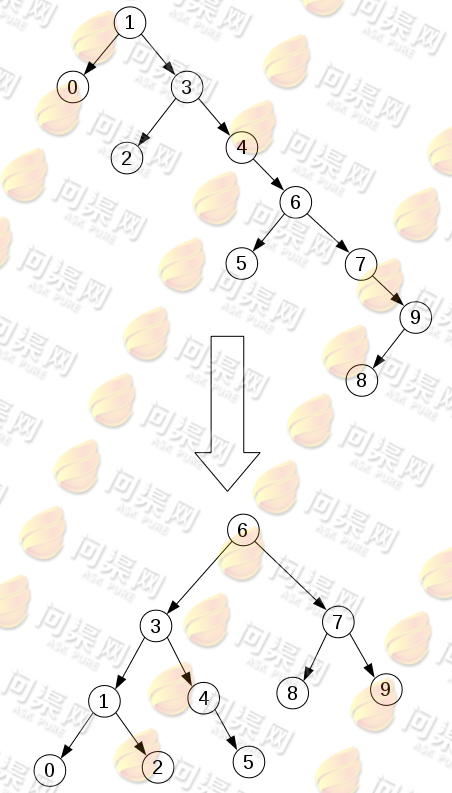
        显然平衡二叉树的查找性能要高于非平衡二叉树，但其节省的查找时间实际上已经消耗在了插入节点的时候。

        本例代码：

code path   chapter.07/e.g.7.4/

https       https://github.com/magicworldos/datastructure.git
git         git@github.com:magicworldos/datastructure.git
subverion   https://github.com/magicworldos/datastructure