数据结构实战

        十字链表可以看作是有向图的邻接表和逆邻接表的组合，每一个弧中存放了这条弧的起始节点索引和终止节点索引，并存放了下一条同起始节点弧指针和下一条同终止节点弧指针。还是以一个有向图来做说明：

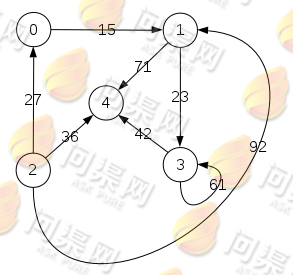
        这个有向图的十字链表如下：

        可以看到：

1. 顶点的两个指针分别存放以此顶点为起点和以此顶点为终点的弧指针。
2. 弧的两个指针分别存放下一个具有相同起点的弧指针和下一个具有相同终点的弧指针。

        它的数据结构定义如下：

//边或弧
typedef struct s_arccell
{
	//权重
	int weight;
	//弧头顶点索引号start vertex index
	int sv_index;
	//弧尾顶点索引号end vertex index
	int ev_index;
	//数据
	void *data;
	//下一个同头弧结节
	struct s_arccell *next_h;
	//下一个同尾弧结节
	struct s_arccell *next_f;

} s_arccell;

typedef struct
{
	//顶点数据
	void *data;
	//出弧，以当前顶点为起始的弧
	s_arccell *arccel_out;
	//入弧，以当前顶点为终止的弧
	s_arccell *arccel_in;
} s_vertex;

//十字链表
typedef struct
{
	//顶点数组
	s_vertex *vertex;
	//顶点个数
	int size;
	//显示顶点数据的回调函数
	void (*visit_vertex)();
	//显示弧数据的回调函数
	void (*visit_arccell)();
} s_graph;

        对于十字链表弧的创建算法如下：

/*
 * 设置边或弧内存的权重及数据
 * int sv_index : 起始顶点索引
 * int ev_index : 终止顶点索引
 * int weight   : 权重
 * void *data   : 数据指针
 */
bool graph_insert_arccell(s_graph *graph, int sv_index, int ev_index, int weight, void *data)
{
	if (graph == null)
	{
		return false;
	}

	if (sv_index < 0 || sv_index >= graph->size)
	{
		return false;
	}

	if (ev_index < 0 || ev_index >= graph->size)
	{
		return false;
	}

	/***
	 * 出入弧
	 */
	//新建一个弧
	s_arccell *arccel = (s_arccell *) malloc(sizeof(s_arccell));
	//弧数据
	arccel->data = data;
	//权重
	arccel->weight = weight;
	//弧尾关联的顶点索引号
	arccel->sv_index = sv_index;
	arccel->ev_index = ev_index;
	arccel->next_h = null;
	arccel->next_f = null;

	//如果顶点中第一条弧为空
	if (graph->vertex[sv_index].arccel_out == null)
	{
		//设置顶点的每一条弧
		graph->vertex[sv_index].arccel_out = arccel;
	}
	else
	{
		//找到顶点弧中最后一条弧
		s_arccell *p = graph->vertex[sv_index].arccel_out;
		while (p->next_h != null)
		{
			p = p->next_h;
		}
		//追加新弧
		p->next_h = arccel;
	}

	//设置顶点的入弧
	if (graph->vertex[ev_index].arccel_in == null)
	{
		graph->vertex[ev_index].arccel_in = arccel;
	}

	//设置下一条同终止顶点指针
	if (graph->arccel_temp[ev_index] != null)
	{
		graph->arccel_temp[ev_index]->next_f = arccel;
	}
	graph->arccel_temp[ev_index] = arccel;

	return true;
}

        编写main函数来创建这个十字链表：

#include <stdio.h>
#include <stdlib.h>
#include "graph.h"

void visit_int(int *i)
{
	if (i != null)
	{
		printf("%d", *i);
	}
}

int main(int argc, char **args)
{
	//邻接表
	s_graph graph;
	graph_init(&graph, 5, &visit_int, &visit_int);

	//顶点数据项
	int *t0 = (int *) malloc(sizeof(int));
	int *t1 = (int *) malloc(sizeof(int));
	int *t2 = (int *) malloc(sizeof(int));
	int *t3 = (int *) malloc(sizeof(int));
	int *t4 = (int *) malloc(sizeof(int));
	//顶点数据
	*t0 = 53;
	*t1 = 43;
	*t2 = 12;
	*t3 = 54;
	*t4 = 75;
	//弧数据项
	int *d0 = (int *) malloc(sizeof(int));
	int *d1 = (int *) malloc(sizeof(int));
	int *d2 = (int *) malloc(sizeof(int));
	int *d3 = (int *) malloc(sizeof(int));
	int *d4 = (int *) malloc(sizeof(int));
	int *d5 = (int *) malloc(sizeof(int));
	int *d6 = (int *) malloc(sizeof(int));
	int *d7 = (int *) malloc(sizeof(int));
	//弧数据
	*d0 = 56;
	*d1 = 34;
	*d2 = 75;
	*d3 = 96;
	*d4 = 77;
	*d5 = 19;
	*d6 = 64;
	*d7 = 58;

	//设置顶点数据
	graph_set_vertex(&graph, 0, t0);
	graph_set_vertex(&graph, 1, t1);
	graph_set_vertex(&graph, 2, t2);
	graph_set_vertex(&graph, 3, t3);
	graph_set_vertex(&graph, 4, t4);

	//插入弧数据
	graph_insert_arccell(&graph, 0, 1, 15, d0);
	graph_insert_arccell(&graph, 1, 3, 23, d1);
	graph_insert_arccell(&graph, 1, 4, 71, d2);
	graph_insert_arccell(&graph, 2, 0, 27, d3);
	graph_insert_arccell(&graph, 2, 1, 92, d4);
	graph_insert_arccell(&graph, 2, 4, 36, d5);
	graph_insert_arccell(&graph, 3, 3, 61, d6);
	graph_insert_arccell(&graph, 3, 4, 42, d7);

	/*
	 * 显示邻接表，格式如下：
	 * [顶点索引, 顶点数据] -> (弧尾指向顶点的索引, 弧权重, 弧数据) -> (弧尾指向顶点的索引, 弧权重, 弧数据)
	 */
	graph_visit(&graph);

	//销毁邻接表
	graph_destroy(&graph);

	return 0;
}

        运行结果：

[0, 53] -> (2, 0, 27, 96) 
[1, 43] -> (0, 1, 15, 56) 
[2, 12]
[3, 54] -> (1, 3, 23, 34) 
[4, 75] -> (1, 4, 71, 75) 


[0, 53] --> {0, 1, 15, 56 -> (2, 1, 92, 77) } 
[1, 43] --> {1, 3, 23, 34 -> (3, 3, 61, 64) }  --> {1, 4, 71, 75 -> (2, 4, 36, 19)  -> (3, 4, 42, 58) } 
[2, 12] --> {2, 0, 27, 96}  --> {2, 1, 92, 77}  --> {2, 4, 36, 19 -> (3, 4, 42, 58) } 
[3, 54] --> {3, 3, 61, 64}  --> {3, 4, 42, 58} 
[4, 75]

        其中花括号{}->{}表示弧节点及下一下相同头顶点弧。在花括号里面的()->()表示下一个相同尾顶点弧。

        本例代码：

code path   chapter.06/e.g.6.3/

https       https://github.com/magicworldos/datastructure.git
git         git@github.com:magicworldos/datastructure.git
subverion   https://github.com/magicworldos/datastructure