数据结构实战

        多重邻接表与十字链表类似，一个边存放两个顶点的索引，并使用两个指针来指向这两个顶点相关的下一条边。以下图为例：

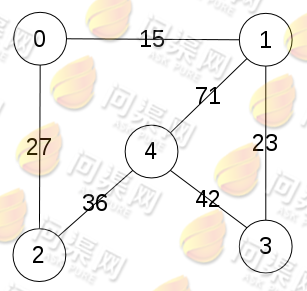
        实现代码如下：

//边
typedef struct s_arccell
{
	//权重
	int weight;
	//边头顶点索引号i vertex index
	int i_index;
	//边尾顶点索引号j vertex index
	int j_index;
	//数据
	void *data;
	//下一个与i相关的边结节
	struct s_arccell *next_i;
	//下一个与j相关的边结节
	struct s_arccell *next_j;

} s_arccell;

typedef struct
{
	//顶点数据
	void *data;
	//第一条与此顶点相关的边
	s_arccell *arccel_first;
} s_vertex;

//多重邻接表
typedef struct
{
	//顶点数组
	s_vertex *vertex;
	//顶点个数
	int size;
	//显示顶点数据的回调函数
	void (*visit_vertex)();
	//显示边数据的回调函数
	void (*visit_arccell)();
} s_graph;

/*
 * 设置边或边内存的权重
 * int i_index : 顶点i索引
 * int j_index : 顶点j索引
 * int weight   : 权重
 * void *data   : 数据指针
 */
bool graph_insert_arccell(s_graph *graph, int i_index, int j_index, int weight, void *data)
{
	if (graph == null)
	{
		return false;
	}

	if (i_index < 0 || i_index >= graph->size)
	{
		return false;
	}

	if (j_index < 0 || j_index >= graph->size)
	{
		return false;
	}

	/***
	 * 出入边
	 */
	//新建一个边
	s_arccell *arccel = (s_arccell *) malloc(sizeof(s_arccell));
	//边数据
	arccel->data = data;
	//权重
	arccel->weight = weight;
	//边尾关联的顶点索引号
	arccel->i_index = i_index;
	arccel->j_index = j_index;
	arccel->next_i = null;
	arccel->next_j = null;

	//如果顶点中第一条边为空
	if (graph->vertex[i_index].arccel_first == null)
	{
		//设置顶点的每一条边
		graph->vertex[i_index].arccel_first = arccel;
	}

	if (graph->vertex[j_index].arccel_first == null)
	{
		//设置顶点的每一条边
		graph->vertex[j_index].arccel_first = arccel;
	}

	if (graph->arccel_temp[j_index] != null)
	{
		graph->arccel_temp[j_index]->next_j = arccel;
	}
	graph->arccel_temp[j_index] = arccel;

	if (graph->arccel_temp[i_index] != null)
	{
		graph->arccel_temp[i_index]->next_i = arccel;
	}
	graph->arccel_temp[i_index] = arccel;

	return true;
}

        main函数如下：

#include <stdio.h>
#include <stdlib.h>
#include "graph.h"

void visit_int(int *i)
{
	if (i != null)
	{
		printf("%d", *i);
	}
}

int main(int argc, char **args)
{
	//邻接表
	s_graph graph;
	graph_init(&graph, 5, &visit_int, &visit_int);

	//顶点数据项
	int *t0 = (int *) malloc(sizeof(int));
	int *t1 = (int *) malloc(sizeof(int));
	int *t2 = (int *) malloc(sizeof(int));
	int *t3 = (int *) malloc(sizeof(int));
	int *t4 = (int *) malloc(sizeof(int));
	//顶点数据
	*t0 = 53;
	*t1 = 43;
	*t2 = 12;
	*t3 = 54;
	*t4 = 75;
	//边数据项
	int *d0 = (int *) malloc(sizeof(int));
	int *d1 = (int *) malloc(sizeof(int));
	int *d2 = (int *) malloc(sizeof(int));
	int *d3 = (int *) malloc(sizeof(int));
	int *d4 = (int *) malloc(sizeof(int));
	int *d5 = (int *) malloc(sizeof(int));
	//边数据
	*d0 = 56;
	*d1 = 34;
	*d2 = 75;
	*d3 = 96;
	*d4 = 19;
	*d5 = 58;

	//设置顶点数据
	graph_set_vertex(&graph, 0, t0);
	graph_set_vertex(&graph, 1, t1);
	graph_set_vertex(&graph, 2, t2);
	graph_set_vertex(&graph, 3, t3);
	graph_set_vertex(&graph, 4, t4);

	//插入边数据
	graph_insert_arccell(&graph, 0, 1, 15, d0);
	graph_insert_arccell(&graph, 1, 3, 23, d1);
	graph_insert_arccell(&graph, 1, 4, 71, d2);
	graph_insert_arccell(&graph, 2, 0, 27, d3);
	graph_insert_arccell(&graph, 2, 4, 36, d4);
	graph_insert_arccell(&graph, 3, 4, 42, d5);

	/*
	 * 显示邻接表，格式如下：
	 * [顶点索引, 顶点数据] -> (边尾指向顶点的索引, 边权重, 边数据) -> (边尾指向顶点的索引, 边权重, 边数据)
	 */
	graph_visit(&graph);

	//销毁邻接表
	graph_destroy(&graph);

	return 0;
}

        运行结果：

[0, 53] --> {0, 1, 15, 56 -> (2, 0, 27, 96) }  --> {1, 3, 23, 34}  --> {3, 4, 42, 58} 
[1, 43] --> {0, 1, 15, 56 -> (2, 0, 27, 96) }  --> {1, 3, 23, 34}  --> {3, 4, 42, 58} 
[2, 12] --> {2, 0, 27, 96}  --> {2, 4, 36, 19 -> (3, 4, 42, 58) } 
[3, 54] --> {1, 3, 23, 34}  --> {3, 4, 42, 58} 
[4, 75] --> {1, 4, 71, 75 -> (2, 4, 36, 19)  -> (3, 4, 42, 58) }

        当然，本例运行结果中所反映出的多重邻接表非常简单。建构图时，不同的构建顺序和顶点顺序对多重邻接表的影响也是非常大的。例如修改main函数中插入边的代码：

//插入边数据
graph_insert_arccell(&graph, 0, 1, 15, d0);
graph_insert_arccell(&graph, 3, 1, 23, d1);
graph_insert_arccell(&graph, 4, 1, 71, d2);
graph_insert_arccell(&graph, 0, 1, 27, d3);
graph_insert_arccell(&graph, 4, 2, 36, d4);
graph_insert_arccell(&graph, 4, 3, 42, d5);

        修改后的运行结果：

[0, 53] --> {0, 1, 15, 56 -> (3, 1, 23, 34)  -> (4, 3, 42, 58) }  --> {0, 2, 27, 96 -> (4, 2, 36, 19) } 
[1, 43] --> {0, 1, 15, 56 -> (3, 1, 23, 34)  -> (4, 3, 42, 58) }  --> {0, 2, 27, 96 -> (4, 2, 36, 19) } 
[2, 12] --> {0, 2, 27, 96 -> (4, 2, 36, 19) } 
[3, 54] --> {3, 1, 23, 34 -> (4, 3, 42, 58) } 
[4, 75] --> {4, 1, 71, 75}  --> {4, 2, 36, 19}  --> {4, 3, 42, 58} 

        只修改了边的两个顶点的顺序，多重邻接表的构建结果就完全不同了，但它们所表示的图完全相同（无向图）。

        本例代码：

code path   chapter.06/e.g.6.4/

https       https://github.com/magicworldos/datastructure.git
git         git@github.com:magicworldos/datastructure.git
subverion   https://github.com/magicworldos/datastructure