数据结构实战
本文作者:李德强
第三节 二叉排序树
在前面学习了二叉树的构建与遍历之后,再学习二叉排序树就简单的多了。二叉排序树的特点为,任意节点的左孩子节点的权值小于其自身权值,其右孩子节点的权值大于其自身权值。我们来看一下二叉排序树的结构:
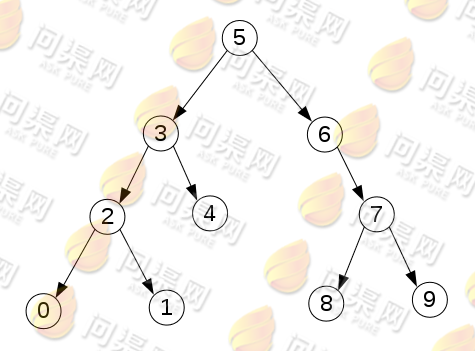
下面我们就来构建这样一棵二叉排序树:
//二叉树节点
typedef struct s_node
{
//权重
int weight;
//父节点
struct s_node *parent;
//左孩子节点
struct s_node *left_child;
//右孩子节点
struct s_node *right_child;
} s_node;
//二叉树数据结构
typedef struct s_tree
{
//根节点
s_node *root;
} s_tree;
我们需要实现一个查找函数,当在二叉排序树中找到权值相同的节点是,显示当前节点,表示已经找到结果。如果没有找到则将当前查找权值作为新节点按二叉排序树的特性插入树中:
//根据val到二叉树中查找
bool tree_search(s_tree *tree, int val)
{
if (tree == null)
{
return false;
}
//如果二叉树没有根节点
if (tree->root == null)
{
//创建权值为val的根节点
s_node *p_new = (s_node *) malloc(sizeof(s_node));
p_new->weight = val;
p_new->parent = null;
p_new->left_child = null;
p_new->right_child = null;
tree->root = p_new;
return true;
}
else
{
//递归查找
return tree_find(tree->root, val);
}
}
//递归查找节点,如果找不到就插入
bool tree_find(s_node *node, int val)
{
if (node == null)
{
return false;
}
//找到节点
if (val == node->weight)
{
printf("Find the node, the value is 3.\n");
}
//如果小于当前节点,则在其左子树上处理
else if (val < node->weight)
{
//如果左子树为空
if (node->left_child == null)
{
s_node *p_new = (s_node *) malloc(sizeof(s_node));
p_new->weight = val;
p_new->parent = node;
p_new->left_child = null;
p_new->right_child = null;
node->left_child = p_new;
return true;
}
//如果当前值大于左子树
else if (val > node->left_child->weight)
{
s_node *p_new = (s_node *) malloc(sizeof(s_node));
p_new->weight = val;
p_new->parent = node;
p_new->left_child = node->left_child;
p_new->right_child = null;
p_new->left_child->parent = p_new;
node->left_child = p_new;
return true;
}
//如果小于左子树
else
{
//递归处理其左子树
return tree_find(node->left_child, val);
}
}
//如果大于当前节点,则在其左子树上处理
else
{
//如果右子树为空
if (node->right_child == null)
{
s_node *p_new = (s_node *) malloc(sizeof(s_node));
p_new->weight = val;
p_new->parent = node;
p_new->left_child = null;
p_new->right_child = null;
node->right_child = p_new;
return true;
}
//如果小于右子树权值
else if (val < node->right_child->weight)
{
s_node *p_new = (s_node *) malloc(sizeof(s_node));
p_new->weight = val;
p_new->parent = node;
p_new->right_child = node->right_child;
p_new->left_child = null;
p_new->right_child->parent = p_new;
node->right_child = p_new;
return true;
}
//如果大于右子树权值
else
{
return tree_find(node->right_child, val);
}
}
return true;
}
再来写一个主函数来测试:
#include <stdio.h>
#include <stdlib.h>
#include "tree.h"
int main(int argc, char **args)
{
//初始化树
s_tree tree;
tree_init(&tree);
tree_search(&tree, 5);
tree_search(&tree, 3);
tree_search(&tree, 4);
tree_search(&tree, 6);
tree_search(&tree, 7);
tree_search(&tree, 2);
tree_search(&tree, 9);
tree_search(&tree, 8);
tree_search(&tree, 0);
tree_search(&tree, 1);
//中序遍历
tree_inorder_visit(&tree, tree.root);
//销毁树
tree_destroy(&tree);
return 0;
}
运行结果:
Node weight is 0. Node weight is 1. Node weight is 2. Node weight is 3. Node weight is 4. Node weight is 5. Node weight is 6. Node weight is 7. Node weight is 8. Node weight is 9.
本例代码:
code path chapter.07/e.g.7.3/ https https://github.com/magicworldos/datastructure.git git git@github.com:magicworldos/datastructure.git subverion https://github.com/magicworldos/datastructure
Copyright © 2015-2023 问渠网 辽ICP备15013245号