数据结构实战

        首先我们来简单的学习一下二叉树的存储结构：

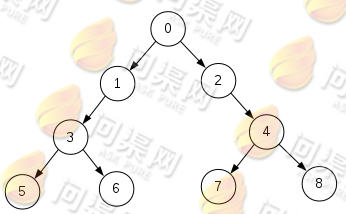
        二叉树是普通树的一种特殊形式，二叉树的每一个数据节点都有一个节点称作父节点（或双亲节点）和两个子节点，称作左孩子和右孩子。当然，对于根节点来说，它的父节点必为空。而对于所有非根节点来说，父节点必然存在。对于最底层叶子节点来说，它们的左右孩子节点必为空。其它节点的左右孩子节点可以为空也可以非空。下面来看一下二叉树的数据结构：

//二叉树节点
typedef struct s_node
{
	//数据指针
	void *data;
	//父节点
	struct s_node *parent;
	//左孩子节点
	struct s_node *left_child;
	//右孩子节点
	struct s_node *right_child;
} s_node;

//二叉树数据结构
typedef struct s_tree
{
	//根节点
	s_node *root;
	//访问函数指针
	void (*visit_node)();
	//释放内存函数指针
	void (*free_node)();
} s_tree;

        接下来实现二叉树的一些常用功能函数：

//初始化树
bool tree_init(s_tree *tree, void (*visit_node)(), void (*free_node)())
{
	if (tree == null)
	{
		return false;
	}

	tree->root = null;
	tree->visit_node = visit_node;
	tree->free_node = free_node;

	return true;
}

//销毁树
bool tree_destroy(s_tree *tree)
{
	if (tree == null)
	{
		return false;
	}

	//清空树
	tree_clear(tree, tree->root);

	//根节点置空
	tree->root = null;

	return true;
}

//清空树
void tree_clear(s_tree *tree, s_node *node)
{
	if (node == null)
	{
		return;
	}

	//递归清空左子树
	tree_clear(tree, node->left_child);
	//递归清空右子树
	tree_clear(tree, node->right_child);

	//如果数据项不为空
	if (node->data != null)
	{
		//释放数据项内存
		tree->free_node(node->data);
	}

	node->left_child = null;
	node->right_child = null;

	if (node == tree->root)
	{
		tree->root = null;
	}

	//释放当前节点内存
	free(node);
}

//取得根节点
s_node* tree_root(s_tree *tree)
{
	if (tree == null)
	{
		return null;
	}

	return tree->root;
}

//找到数据项在树中的节点
bool tree_find_node(s_node *node, s_node **node_f, void *data)
{
	if (node == null)
	{
		return false;
	}

	if (node_f == null)
	{
		return false;
	}

	if (data == null)
	{
		return false;
	}

	//找到同地址数据项，返回当前节点
	if (node->data == data)
	{
		*node_f = node;
		return true;
	}

	//递归查找左子树
	if (tree_find_node(node->left_child, node_f, data))
	{
		return true;
	}
	//递归查找右子树
	if (tree_find_node(node->right_child, node_f, data))
	{
		return true;
	}

	return false;
}

//找到数据项在树中的父节点
s_node* tree_parent(s_tree *tree, void *data)
{
	if (tree == null)
	{
		return null;
	}

	if (data == null)
	{
		return null;
	}

	//找到数据项所在的节点
	s_node *node_find = null;
	tree_find_node(tree->root, &node_find, data);
	if (node_find == null)
	{
		return null;
	}

	//返回父节点
	return node_find->parent;
}

//找到数据项在树中的左孩子
s_node* tree_left_child(s_tree *tree, void *data)
{
	if (tree == null)
	{
		return null;
	}

	if (data == null)
	{
		return null;
	}

	//找到数据项所在的节点
	s_node *node_find = null;
	tree_find_node(tree->root, &node_find, data);
	if (node_find == null)
	{
		return null;
	}

	//返回左孩子节点
	return node_find->left_child;
}

//找到数据项在树中的右孩子
s_node* tree_right_child(s_tree *tree, void *data)
{
	if (tree == null)
	{
		return null;
	}

	if (data == null)
	{
		return null;
	}

	//找到数据项所在的节点
	s_node *node_find = null;
	tree_find_node(tree->root, &node_find, data);
	if (node_find == null)
	{
		return null;
	}

	//返回右孩子节点
	return node_find->right_child;
}

//找到数据项在树中的左兄弟
s_node* tree_left_brother(s_tree *tree, void *data)
{
	if (tree == null)
	{
		return null;
	}

	if (data == null)
	{
		return null;
	}

	//找到数据项所在的节点
	s_node *node_find = null;
	tree_find_node(tree->root, &node_find, data);
	if (node_find == null)
	{
		return null;
	}

	if (node_find->parent == null)
	{
		return null;
	}

	if (node_find == node_find->parent->left_child)
	{
		return null;
	}

	//返回左兄弟
	return node_find->parent->left_child;
}

//找到数据项在树中的右兄弟
s_node* tree_right_brother(s_tree *tree, void *data)
{
	if (tree == null)
	{
		return null;
	}

	if (data == null)
	{
		return null;
	}

	//找到数据项所在的节点
	s_node *node_find = null;
	tree_find_node(tree->root, &node_find, data);
	if (node_find == null)
	{
		return null;
	}

	if (node_find->parent == null)
	{
		return null;
	}

	if (node_find == node_find->parent->right_child)
	{
		return null;
	}

	//返回右兄弟
	return node_find->parent->right_child;
}

//将node_ins插入node的左或右节点，原节点做为node_ins的右节点
bool tree_insert(s_tree *tree, s_node *node, int leftright, s_node *node_ins)
{
	if (tree == null)
	{
		return false;
	}

	if (node_ins == null)
	{
		return false;
	}

	//如果是一棵空树
	if (tree->root == null)
	{
		//将节点做为树的根节点
		tree->root = node_ins;
		node_ins->parent = null;
		return true;
	}

	//被插入节点的右子树必须为空
	if (node_ins->right_child != null)
	{
		return false;
	}

	//如果插入目标节点的左节点
	if (leftright == 0)
	{
		//插入左节点
		s_node *p_temp = node->left_child;
		node->left_child = node_ins;
		node_ins->parent = node;
		//将原左子树挂接到新节点的右子树上
		node_ins->right_child = p_temp;
		if (p_temp != null)
		{
			p_temp->parent = node_ins;
		}
	}
	//如果插入目标节点的右节点
	else if (leftright == 1)
	{
		//插入右节点
		s_node *p_temp = node->right_child;
		node->right_child = node_ins;
		node_ins->parent = node;
		//将原右子树挂接到新节点的右子树上
		node_ins->right_child = p_temp;
		if (p_temp != null)
		{
			p_temp->parent = node_ins;
		}
	}

	return true;
}

//删除节点
void tree_delete_node(s_tree *tree, s_node *node)
{
	if (node == null)
	{
		return;
	}

	//递归删除左子树
	tree_delete_node(tree, node->left_child);
	//递归删除右子树
	tree_delete_node(tree, node->right_child);

	if (node->data != null)
	{
		tree->free_node(node->data);
	}

	//删除左节点
	node->left_child = null;
	//删除右节点
	node->right_child = null;

	//如果是根节点则清空树
	if (node == tree->root)
	{
		tree->root = null;
	}

	free(node);
}

//删除树的节点
bool tree_delete(s_tree *tree, s_node *node, int leftright)
{
	if (tree == null)
	{
		return false;
	}

	if (node == null)
	{
		return false;
	}

	//删除左子树
	if (leftright == 0)
	{
		tree_delete_node(tree, node->left_child);
		node->left_child = null;
	}
	//删除右子树
	else if (leftright == 1)
	{
		tree_delete_node(tree, node->right_child);
		node->right_child = null;
	}

	//如果是根节点则清空树
	if (node == tree->root)
	{
		tree->root = null;
	}

	return true;
}

        对于树这种数据结构来说，很多函数通常都使用递归来实现的，这与树的数据结构一致。因为树的一个叶子节点可以看做是另外一棵树，而这棵树的每一个节点同样也都可以看作是另外的树。

        最后来编写一个main函数对二叉树的数据结构做一些测试：

//删除整数函数
void free_int(int *i)
{
	if (i != null)
	{
		free(i);
	}
}

//访问整数函数
void visit_int(int *i)
{
	if (i != null)
	{
		printf("%d", *i);
	}
}

int main(int argc, char **args)
{
	int *t0 = (int *) malloc(sizeof(int));
	int *t1 = (int *) malloc(sizeof(int));
	int *t2 = (int *) malloc(sizeof(int));

	*t0 = 0;
	*t1 = 1;
	*t2 = 2;

	//初始化树
	s_tree tree;
	tree_init(&tree, &visit_int, &free_int);

	s_node *n0 = (s_node *) malloc(sizeof(s_node));
	s_node *n1 = (s_node *) malloc(sizeof(s_node));
	s_node *n2 = (s_node *) malloc(sizeof(s_node));

	n0->parent = null;
	n0->left_child = null;
	n0->right_child = null;
	n0->data = t0;

	n1->parent = null;
	n1->left_child = null;
	n1->right_child = null;
	n1->data = t1;

	n2->parent = null;
	n2->left_child = null;
	n2->right_child = null;
	n2->data = t2;

	//插入根节点
	s_node *node = tree.root;
	tree_insert(&tree, node, 0, n0);
	//插入根节点的左孩子
	node = tree.root;
	tree_insert(&tree, node, 0, n1);
	//插入根节点的右孩子
	node = tree.root;
	tree_insert(&tree, node, 1, n2);

	//得到根节点
	s_node *p = tree_root(&tree);
	visit_int(p->data);
	printf("\n");

	//得到父节点
	p = tree_parent(&tree, t1);
	visit_int(p->data);
	printf("\n");

	//得到父节点
	p = tree_parent(&tree, t2);
	visit_int(p->data);
	printf("\n");

	//得到左孩子
	p = tree_left_child(&tree, t0);
	visit_int(p->data);
	printf("\n");

	//得到右孩子
	p = tree_right_child(&tree, t0);
	visit_int(p->data);
	printf("\n");

	//得到左兄弟
	p = tree_left_brother(&tree, t2);
	visit_int(p->data);
	printf("\n");

	//得到右兄弟
	p = tree_right_brother(&tree, t1);
	visit_int(p->data);
	printf("\n");

	//删除根节点的左孩子
	tree_delete(&tree, tree.root, 0);
	p = tree_left_child(&tree, t0);
	if (p == null)
	{
		printf("Left child of the root node is null.\n");
	}

	//删除根节点的右孩子
	tree_delete(&tree, tree.root, 1);
	p = tree_right_child(&tree, t1);
	if (p == null)
	{
		printf("Right child of the root node is null.\n");
	}

	//销毁树
	tree_destroy(&tree);

	return 0;
}

        运行结果：

0
0
0
1
2
1
2
Left child of the root node is null.
Right child of the root node is null.

        本例代码：

code path   chapter.05/e.g.5.1/

https       https://github.com/magicworldos/datastructure.git
git         git@github.com:magicworldos/datastructure.git
subverion   https://github.com/magicworldos/datastructure