数据结构实战

          第四节 树与森林

 

 

        树与森林通常为人们在实际生活中对事物的感观认知，例如中国有很多个省，每个省中又有多个城市，每个成都市中又被划分出多个区、县等等。又如一个公司有多个事业部，每一个事业部下又有多个部门，每个部门中又有多个业务方向等等。我们把这类数据抽象为“树”型结构。多个树被称之为森林。我们可以使用图形来表示树和森林的结构：

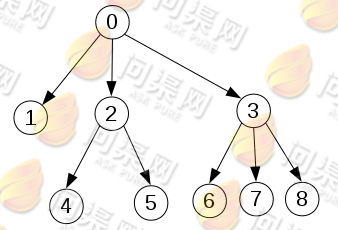
树（多叉树）

森林（多叉树森林）

        为了与二叉树区分开来，普通的树型结构通常称为多叉树。它的表示方法也有很多，例如父节点表示法：

typedef struct s_node
{
	//数据指针
	void *data;
	//父节点
	struct s_node *parent;	
} s_node;

        或者采用孩子节点表示法：

typedef struct s_node
{
	//数据指针
	void *data;
	//孩子节点
	struct s_node* children[MAX_COUNT];	
} s_node;

        或者采用父子节点表示法：

typedef struct s_node
{
	//数据指针
	void *data;
	//父节点
	struct s_node *parent;	
	//孩子节点
	struct s_node *children[MAX_COUNT];	
} s_node;

        这几种数据结构都可以表示多叉树。但它们有都一些局限性，构建树操作和遍历树操作都相对复杂。

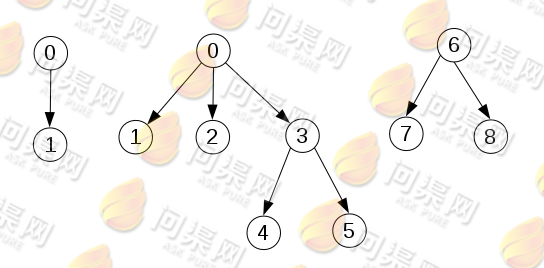
        对于多叉树和森林，通常还有另外一种比较好的表示方法，叫做：孩子兄弟表示法，或者叫二叉树表示法，或者叫二叉链表表示法。这种表示方法是将树或森林转化为通用二叉树来表示。二叉树中左节点表示当前节点的孩子节点，右节点表示当前节点的兄弟节点。任何一个多叉树或森林都可以采用这种方式转化为一棵二叉树：

多叉树转化为二叉树表示

森林转化为二叉树表示

 

        二叉树中左节点表示多叉树中子节点，二叉树中右节点表示多叉树中的兄弟节点：

//二叉树节点
typedef struct s_node
{
	//数据指针
	void *data;
	//父节点
	struct s_node *parent;
	//左孩子节点
	struct s_node *left_child;
	//右兄弟节点
	struct s_node *right_sibling;
} s_node;

//二叉树数据结构
typedef struct s_tree
{
	//根节点
	s_node *root;
	//访问函数指针
	void (*visit_node)();
	//释放内存函数指针
	void (*free_node)();
} s_tree;

        在前面的章节中我们已经学习二叉树的相关操作，这里就可以使用直接使用二叉树来表示多叉树与森林：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "tree.h"

//删除整数函数
void free_int(int *i)
{
	if (i != null)
	{
		free(i);
	}
}

//访问整数函数
void visit_int(int *i)
{
	if (i != null)
	{
		printf("%d ", *i);
	}
}

//多叉树的二叉树表示法
void sample_A()
{
	int *t0 = (int *) malloc(sizeof(int));
	int *t1 = (int *) malloc(sizeof(int));
	int *t2 = (int *) malloc(sizeof(int));
	int *t3 = (int *) malloc(sizeof(int));
	int *t4 = (int *) malloc(sizeof(int));
	int *t5 = (int *) malloc(sizeof(int));
	int *t6 = (int *) malloc(sizeof(int));
	int *t7 = (int *) malloc(sizeof(int));
	int *t8 = (int *) malloc(sizeof(int));

	*t0 = 0;
	*t1 = 1;
	*t2 = 2;
	*t3 = 3;
	*t4 = 4;
	*t5 = 5;
	*t6 = 6;
	*t7 = 7;
	*t8 = 8;

	//初始化树
	s_tree tree;
	tree_init(&tree, &visit_int, &free_int);

	s_node *n0 = (s_node *) malloc(sizeof(s_node));
	s_node *n1 = (s_node *) malloc(sizeof(s_node));
	s_node *n2 = (s_node *) malloc(sizeof(s_node));
	s_node *n3 = (s_node *) malloc(sizeof(s_node));
	s_node *n4 = (s_node *) malloc(sizeof(s_node));
	s_node *n5 = (s_node *) malloc(sizeof(s_node));
	s_node *n6 = (s_node *) malloc(sizeof(s_node));
	s_node *n7 = (s_node *) malloc(sizeof(s_node));
	s_node *n8 = (s_node *) malloc(sizeof(s_node));

	tree_init_node(n0, t0);
	tree_init_node(n1, t1);
	tree_init_node(n2, t2);
	tree_init_node(n3, t3);
	tree_init_node(n4, t4);
	tree_init_node(n5, t5);
	tree_init_node(n6, t6);
	tree_init_node(n7, t7);
	tree_init_node(n8, t8);

	//插入根节点
	tree_insert(&tree, null, 0, n0);
	tree_insert(&tree, n0, 0, n1);
	tree_insert(&tree, n1, 1, n2);
	tree_insert(&tree, n2, 0, n4);
	tree_insert(&tree, n2, 1, n3);
	tree_insert(&tree, n4, 1, n5);
	tree_insert(&tree, n3, 0, n6);
	tree_insert(&tree, n6, 1, n7);
	tree_insert(&tree, n7, 1, n8);

	//前序遍历
	tree_preamble_visit(&tree, tree.root);
	printf("\n");
	//中序遍历
	tree_inorder_visit(&tree, tree.root);
	printf("\n");
	//后序遍历
	tree_postorder_visit(&tree, tree.root);
	printf("\n");

	//销毁树
	tree_destroy(&tree);
}

//森林的二叉树表示法
void sample_B()
{
	int *t0 = (int *) malloc(sizeof(int));
	int *t1 = (int *) malloc(sizeof(int));
	int *t2 = (int *) malloc(sizeof(int));
	int *t3 = (int *) malloc(sizeof(int));
	int *t4 = (int *) malloc(sizeof(int));
	int *t5 = (int *) malloc(sizeof(int));
	int *t6 = (int *) malloc(sizeof(int));
	int *t7 = (int *) malloc(sizeof(int));
	int *t8 = (int *) malloc(sizeof(int));

	*t0 = 0;
	*t1 = 1;
	*t2 = 2;
	*t3 = 3;
	*t4 = 4;
	*t5 = 5;
	*t6 = 6;
	*t7 = 7;
	*t8 = 8;

	//初始化树
	s_tree tree;
	tree_init(&tree, &visit_int, &free_int);

	s_node *n0 = (s_node *) malloc(sizeof(s_node));
	s_node *n1 = (s_node *) malloc(sizeof(s_node));
	s_node *n2 = (s_node *) malloc(sizeof(s_node));
	s_node *n3 = (s_node *) malloc(sizeof(s_node));
	s_node *n4 = (s_node *) malloc(sizeof(s_node));
	s_node *n5 = (s_node *) malloc(sizeof(s_node));
	s_node *n6 = (s_node *) malloc(sizeof(s_node));
	s_node *n7 = (s_node *) malloc(sizeof(s_node));
	s_node *n8 = (s_node *) malloc(sizeof(s_node));

	tree_init_node(n0, t0);
	tree_init_node(n1, t1);
	tree_init_node(n2, t2);
	tree_init_node(n3, t3);
	tree_init_node(n4, t4);
	tree_init_node(n5, t5);
	tree_init_node(n6, t6);
	tree_init_node(n7, t7);
	tree_init_node(n8, t8);

	//插入根节点
	tree_insert(&tree, null, 0, n0);
	tree_insert(&tree, n0, 0, n1);
	tree_insert(&tree, n1, 1, n2);
	tree_insert(&tree, n2, 0, n3);
	tree_insert(&tree, n2, 1, n6);
	tree_insert(&tree, n3, 1, n4);
	tree_insert(&tree, n4, 1, n5);
	tree_insert(&tree, n6, 0, n7);
	tree_insert(&tree, n7, 1, n8);

	//前序遍历
	tree_preamble_visit(&tree, tree.root);
	printf("\n");
	//中序遍历
	tree_inorder_visit(&tree, tree.root);
	printf("\n");
	//后序遍历
	tree_postorder_visit(&tree, tree.root);
	printf("\n");

	//销毁树
	tree_destroy(&tree);
}

int main(int argc, char **args)
{
	sample_A();

	printf("\n");

	sample_B();

	return 0;
}

        运行结果：

0 1 2 4 5 3 6 7 8 
1 4 5 2 6 7 8 3 0 
5 4 8 7 6 3 2 1 0 

0 1 2 3 4 5 6 7 8 
1 3 4 5 2 7 8 6 0 
5 4 3 8 7 6 2 1 0 

        本例代码：

code path   chapter.05/e.g.5.4/

https       https://github.com/magicworldos/datastructure.git
git         git@github.com:magicworldos/datastructure.git
subverion   https://github.com/magicworldos/datastructure