玩转树莓派
接下来我们要对自平衡算法做一下详细描述。假设有这样一个情景(小时候我们都玩过的):如果有一根很高的木棍直立在你的手掌上,当木棍顶端向前倾斜时,想要让其恢复平衡状态,我们需要将手掌也向前移动,如下:
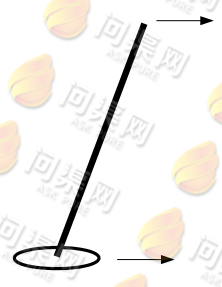
我们来看以下三种情况:
1、木棍顶端前倾的速度大于手掌前移的速度,木棍则继续前倾,直到倒下。
2、木棍顶端前倾的等于大于手掌前移的速度,木棍则保持前倾状态。
3、木棍顶端前倾的速度小于手掌前移的速度,木棍则上扬。
因此我们需要使手掌的速度大于木棍顶端前倾的速度。但我们无法直接测量木棍前倾速度,而是通过MPU6050陀螺仪来测量其倾斜的角加速度进而计算出其倾斜角度。并根据倾斜角度通过PID反馈控制来修正电机正反转数,来实时调整小车的平衡。当然只调整电机速度是不行的,我们需要调整电机的加速度,通过加速度计算出速度:
void engine_move(s_engine *e)
{
//时间片
double timer = (double) ENG_TIMER / 100.0;
//根据初速度、加速度算计当前速度
e->vel = e->vel + e->acc * timer;
}
关于PID控制的资料有很多,我们也不需要作过多的介绍,只对比例(P)、积分(I)、微分(D)各项做一点简单的说明:
比例控制:比例控制器的输出与输入误差信号成比例关系。也就是线性关系。
积分控制:如果在进入稳态后存在稳态误差,则称这个控制系统是有稳态误差的或简 称有差系统。为了消除稳态误差,在控制器中必须引入积分项。积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。
微分控制:在微分控制中,控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系。
一般来说PID控制分为位置式控制和增量式控制,本例所使用的是增量式控制,对PID式子化简,并从Timer的N到时N-1的计算如下(化简过程略):
Acc = Kp * (et - et_1) + (Ki * et) + Kd * (et - 2 * et_1 + et_2)
下面来看一下引擎中自平衡原理:
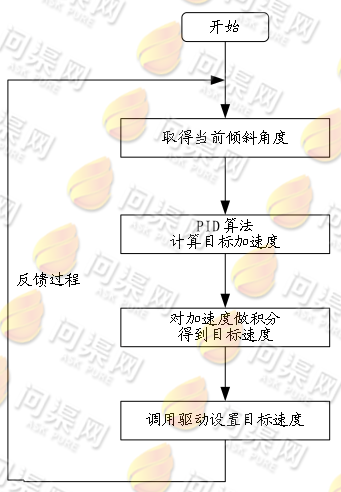
代码实现:
void engine_balance()
{
s_engine *e = &engine;
//启动MPU6050
mpu6050_setup();
//增量式PID输入
double et = 0.0, et_1 = 0.0, et_2 = 0.0;
//启动引擎
while (true)
{
//取得角度
mpu6050_value(&e->x, &e->y, &e->z, &e->ax, &e->ay, &e->az);
//计算倾斜角
double angle = e->y + e->dy;
et_2 = et_1;
et_1 = et;
et = angle;
//PID反馈控制
e->acc = engine_pid(et, et_1, et_2);
//显示输出
printf("angle: %7.2f\tacc: %7.2f\tvel: %7.2f\tKp: %7.2f\tKi: %7.2f\tKd: %7.2f\n", angle, e->acc,e->vel, Kp, Ki, Kd);
//通过电机加速度计算电机速度
engine_move(e);
//设定电机速度
driver_set_speed(e->vel);
//时间片
usleep(ENG_TIMER * 1000);
}
}
接下来需要确定PID中三个系数的值。你可以使用示波器,也可以自己编写图形化界面自己绘制波形。我们在这里只是简单的通过对小车倾斜做观察从而确定了系数取值(没有投入更多的精力使其完美的平衡)。这里我们给出小车的PID参考值为:
Kp = 3989.00; Ki = 216.00; Kd = 32875.00;
最后,非常感谢大家的支持!提供完整的程序代码(Linux 环境 gcc 5.3.1):
Copyright © 2015-2023 问渠网 辽ICP备15013245号