机器学习笔记
本文作者:李德强
第四节 多元线性回归
在实际问题中,随机变量Y往往与多个普通变量x0,x1,x2,x3,...,xn (x0 = 1)有关,对于自变量x0,x1,x2,x3,...,xn的一组确定的值,Y有它的分布,若Y的数学期望存在,则它是x0,x1,x2,x3,...,xn的函数,也就是Y关于x的回归函数:

其中b0,b1,b2,...bn都是与x无关的未知参数。为了使下面的式子达到最小:

求Q分别关于b0,b1,b2,...,bn的偏导数,并令它们等于零,得

化简得:

为了求解方便,将上面式子写成矩阵形式,设:

因:


于是有:

将两边同是左乘 的逆矩阵
的逆矩阵 (设其逆矩阵存在)得:
(设其逆矩阵存在)得:
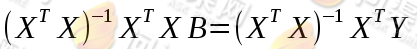
等号左侧化简之后剩余B,于是有

最终我们得到了参数向量B的计算方式,与梯度下降相比,矩阵法的好处是可以不通过反复迭代训练样本,而可以通过样本数据直接计算出回归参数。
Copyright © 2015-2023 问渠网 辽ICP备15013245号